

|
|
 |
|
|
|
||
|
|
|
|
|
(Domain function)† ††††††
(Range function) †††††††††
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
... |
|
k |
2 |
3 |
4 |
5 |
5 |
6 |
7 |
7 |
8 |
9 |
9 |
... |
|
|
3 |
5 |
7 |
0 |
11 |
13 |
0 |
17 |
19 |
0 |
23 |
... |
![]()
. Example:
![]()
††††††††††††††††††††††† ††††††††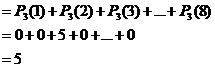
|
k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
... |
|
|
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
... |
This program "![]() "is for testing the formula
"
"is for testing the formula
"![]() "
from part (22.6.1). The purpose of this program is calculating the prime number
"k-th".
"
from part (22.6.1). The purpose of this program is calculating the prime number
"k-th".


. Riemann's Zeta Function
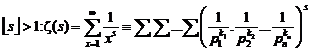
. Riemann's Zeta
equation"![]() "
"
![]()
†The determining of the number of the prime numbers less
than or equal any arbitrary number "p" exactly![]() :
:
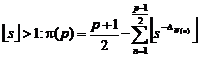
. Example
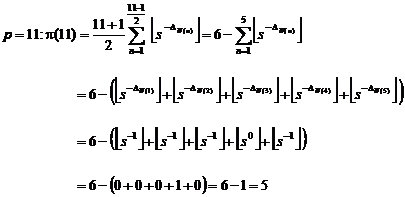
|
P |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
... |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
... |
This program (![]() ) is for testing part (22.8.3).
) is for testing part (22.8.3).
The purpose of this program is determining the number of the
prime numbers before![]() . For example, if you enter a
prime number like
. For example, if you enter a
prime number like![]() , the program will give you
number "6" in answer that shows number
, the program will give you
number "6" in answer that shows number
![]() †is
†is
![]() †prime number.
†prime number.


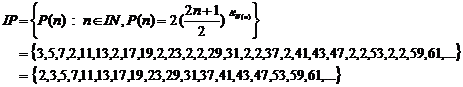
. Example
|
P=2: |
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
... |
|
|
3 |
5 |
7 |
2 |
11 |
13 |
2 |
17 |
19 |
2 |
23 |
2 |
2 |
29 |
31 |
2 |
2 |
... |
This program (![]() ) is for testing (22.10). The
purpose of this program is determining the prime number set. In below form:
) is for testing (22.10). The
purpose of this program is determining the prime number set. In below form:
![]()


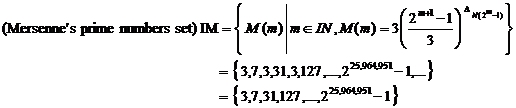
On February 18, 2005, Dr. Martin Nowak from Germany, found
the new largest known prime number,![]() . The prime number has 7,816,230
digits! It took more than 50 days of calculations on Dr. Nowak's 2.4 GHz
Pentium 4 computer. The new prime was independently verified in 5 days by Tony
Reix of Grenoble, France using a 16 Itanium CPU Bull NovaScale 5000 HPC running
the Glucas program by Guillermo Ballester Valor of Granada, Spain. A second
verification was completed by Jeff Gilchrist of Elytra Enterprises Inc. In Ottawa,
Canada using 15 days of time on 12 CPUs of a Compaq Alpha GS160 1.2 GHz CPU
server at SHARCNET.
. The prime number has 7,816,230
digits! It took more than 50 days of calculations on Dr. Nowak's 2.4 GHz
Pentium 4 computer. The new prime was independently verified in 5 days by Tony
Reix of Grenoble, France using a 16 Itanium CPU Bull NovaScale 5000 HPC running
the Glucas program by Guillermo Ballester Valor of Granada, Spain. A second
verification was completed by Jeff Gilchrist of Elytra Enterprises Inc. In Ottawa,
Canada using 15 days of time on 12 CPUs of a Compaq Alpha GS160 1.2 GHz CPU
server at SHARCNET.
Dr. Martin Nowak, an eye surgeon in Michelfeld, Germany learned of GIMPS in April 1999 when he red an article his newspaper, the "Frankfurter Allgemeine Zeitung". Dr. Nowak, a math hobbyist, started with one PC and as his practice grew so did his participation in GIMPS. Six years later, he has 24 computers doing calculations for GIMPSóand one Mersenne Prime to his credit!
Perfectly Scientific, Dr. Crandall's company which developed the FFT algorithm used by GIMPS, makes a poster you can order containing the entire number. It is kind of pricey because accurately printing an over-sized poster in 1-point font is not easy! Makes a cool present for the serious math nut in your family.
Dr. Nowak could not have made this discovery alone. In recognition of contributions made by tens of thousands GIMPS volunteers, credit for this new discovery will go to "Nowak, Woltman, Kurowski, et al". The discovery is the eighth record prime for the GIMPS project. Join now and you could find the next record-breaking prime! You could even win some cash.
For more information on this latest prime discovery read the full press release.
For determining the generating function of an unknown large
enough prime number on other word the generating function of the numbers
greater than the greatest prime number which is the "42nd" known
Mersenne prime namely "![]() " is defined as follows:
" is defined as follows:
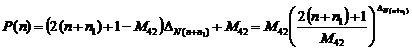 †††††† (1)
†††††† (1)
![]()
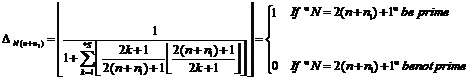
Therefore, the following functions produce either![]() , which is the
greatest known prime number or the prime numbers after this number:
, which is the
greatest known prime number or the prime numbers after this number:
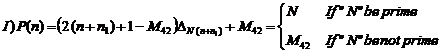
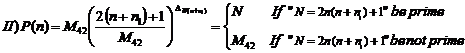
The function in (1) is introduced as the generating function of the unknown large enough prime numbers.
In order to find a prime number large enough by using a computer, there are a lot of algorithms. Each of these algorithms because of its digital inherence is not able to distinguish the prime numbers after a specific large number. So, we should define a function which is able to produce the numbers greater than the greatest known prime number. The following function is a kind of these functions:
![]() ††† (2)
††† (2)
Prime Numbers formula 8 part of source code of the programs of above mentioned article of
The discovery of prime numbers formula and its results that for the first time in the world
we are presenting the source code of the programs by Seyyed Alireza Hashemi Moosavi.
So we are beginning to represent the source code of programs as it is told in the Article of
The Discovery of on-to generating function of the prime numbers and its results.
The 2300 years old unsolvable problem is now solved forever.
Discoverer: Prof.Seyyed Mohammadreza Hashemi Moosavi
1.The
distinction program of the prime numbers![]() and the source code of
the
and the source code of
the
program by Seyyed Alireza Hashemi Moosavi based on the Article by
Prof.Seyyed Mohammadreza Hashemi Moosavi.
This program"![]() "
is for testing the formula
"
is for testing the formula![]() .The
purpose of this program is distinction of
.The
purpose of this program is distinction of
prime numbers. With running this program when the program require to enter a number, then
enter a number, and press the enter key, so the program will tell you that this number is prime or not.



2. The program of the prime numbers
generator (![]() )and the source code of the program
)and the source code of the program
by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.



3.The definition of the prime numbers set by using the on-to generating function of the prime umbers
source code of the program by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.



4.The definition of the Mersenne prime numbers set by using the prime numbers generator
source code of the program by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.



5. The determining of the k-th prime number source code of the program
by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.



6. Solution to the Riemann Zeta equation and determining of the numbers of the prime numbers
less than or equal to any arbitrary number p exactly for p>2 source code of the program
by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.



7. The examination of the guesses of Goldbuch and hardy source cod of the program
by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.
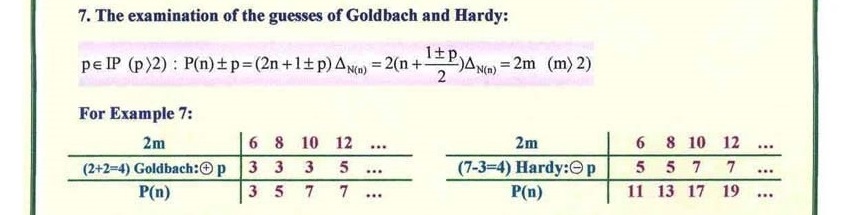


8.The proof of being infinite number of the prime twin couples source code of the program
by Seyyed Alireza Hashemi Moosavi based on the Article
by Prof.Seyyed Mohammadreza Hashemi Moosavi.




Note. This program
designed for determining of the power of new Mersenneís prime
number (Power "p" in ![]() by
using of previous Mersenneís prime numbers power). Here, look at
the part of program and running its results. It dose contain
"25" pages and about "500" lines.
by
using of previous Mersenneís prime numbers power). Here, look at
the part of program and running its results. It dose contain
"25" pages and about "500" lines.
source code by Seyyed Alireza Hashemi Moosavi.








Click here to freely download prime numbers formula program. Open source code by Seyyed Alireza Hashemi Moosavi based on H.M formula. Prime numbers formula was discovered by Professor Seyyed Mohammadreza Hashemi Moosavi on 5th August 2003 .

Note :
Prime numbers
formula is one of the on-to generating functions for the
prime numbers that for every natural number of "m" it
generates all the prime numbers
in order (3,5,7,2,11,13,2,17,19, ...).
The presented "H.M"
functions by discoverer (Prof. Seyyed Mohammad Reza
Hashemi Moosavi) are six number that four
functions are by Wilson's theorem and one of them by Euler's function(
Note :
In Year of 2007 (AAAS)
"
National Association Of Academies
Of Science " (USA)
Awarded A++ grade (Equals to
excellent) to the prime numbers formula and its results by
Prof S.M.R Hashemi Moosavi.
Note :
The
discovery of prime numbers formula and its results has
been published under an article in journal of "Roshd
of Borhan " associated with the Ministry of
Education in Iran.

Note :
You are just permitted to use the subject with
mentioning the reference address of the
Site. All rights reserved to
web designer Seyyed Alireza
Hashemi Moosavi
&
www.primenumbersformula.com
![]()
![]()
![]() )
and another one by sigma(
)
and another one by sigma(
![]() )
functions
and bracket (
)
functions
and bracket (![]() ) functions are discovered by discoverer and the software of
this function is lately produced.
) functions are discovered by discoverer and the software of
this function is lately produced.![]()
![]()
![]()
|
|
More explain about discovery of prime numbers formula |
Infinity proof of prime numbers being was propound 300 years B.C. by Euclid and since that time great mathematicians like Euler tried to discover a formula to produce prime numbers. Many of other mathematicians after many other researches finally found that discovery of prime numbers formula is impossible and this problem will be unsolvable. This discovery shows that one of the complicated and unsolvable problems of mathematics was solved and this discovery proves that there could be no unsolvable problem. I spent twenty years of my life researching and I found this fact that I can't comeback from this path which I came through and I promised myself to keep on searching for the rest of my life to find the solution even if I couldn't achieve the proof.
![]()
|
|
How to use this formula in mathematics and other sciences? |
One of the results of discovering the prime numbers formula is to achieve the solution of Riemann Zeta equation which is on of the popular universal unsolvable problems in mathematics and it's solution needs to achieve the number of the prime numbers for any desirable number of N carefully (with prime numbers formula). Another result is to determine k-th desirable prime number and other uses are definition of prime numbers set, proof of infinity of twin prime pairs considering to the conjectures of Gold Bach and Hardy, find the generator formula for Mersenne prime numbers and also very unknown and big prime numbers and other problems related to prime numbers. In fact the main use of this formula is in coding and decoding that usually use from very big prime numbers for this reason and in the past it was necessary to gain them with complicated mathematics methods and had a hard way to pass through But with presenting of prime numbers formula, definition of coding and decoding systems became easy and convenient.
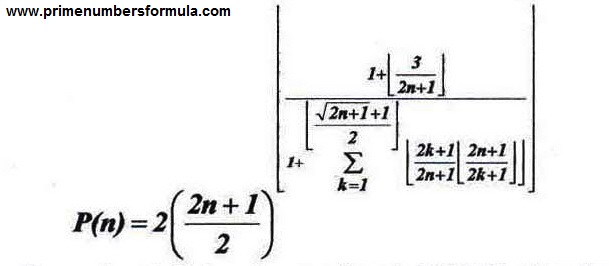
After Euclidís theory about infinite prime numbers in 300 B.C. Most of the mathematicians and other researchers have been curious to find a formula which could generates prime numbers. After many years later some mathematicians like Euler and Fermat presented some formulas to generate prime numbers limitedly. Great mathematicians like Hardy and Courant and many other researchers finally officially announced that such a formula canít be found and to prove their wrong idea they started to publish some Algebraic theorems in their books. Furthermore, determining the number of prime numbers was very important problem. So Gauss and other mathematicians started to set some tables for them. We knew that so far there was no exact formula to determine the number of prime numbers exactly. This problem is known as Zeta Riemann equation which was one of the seven known unsolvable problems of the world that after my discovery on 5th August 2003, one of them is no more unsolvable with the prime numbers formula accurately you can absolutely generate all prime numbers to the nth one. Its consequent generate of prime numbers formula resulted in defining the set of prime numbers and so many other unbelievable results until now like breaking the code of RSA and AES by the use of prime numbers formula and other sets like Mersenne prime, perfect numbers and so many important sets and results just related to the field of number theory and basic sciences.
Discovery of prime numbers formula by Prof. Seyyed Mohammadreza Hashemi Moosavi caused so many results in basic sciences that we will mention part of it in follow:
1. Distinction of prime numbers.
2. Defining a formula for generating prime numbers.
3. Definition of prime numbers set by using the generating function of prime numbers.
4. Defining a formula to generate the Mersenne prime numbers.
5. Determination of Nth prime number.
6. Solving Riemann Zeta equation by using the determination of the number of prime number less than or equal to arbitrary number N exactly.
7. The proof of guesses of Gold Buch and Hardy.
8. The proof of infinity of the prime twin couples.
9. Determining a general series of answer for Diophantine equations.
10. This formula has so many unknown applications in Cryptography, generating Titan Mersenne prime numbers and other sciences like solving NP.
ALL rights reserved - © Copy Right 2003-2023
This site was last updated 06/27/23