Article

This site was last updated 2023-06-27 19:14:11 +0330

Home
Contents of The Book
About Me
Article
Books
Photo Gallery
Contact

 

horizontal rule

January 24, 2010

Breaking the code - How to determine large and very large Primes?

 

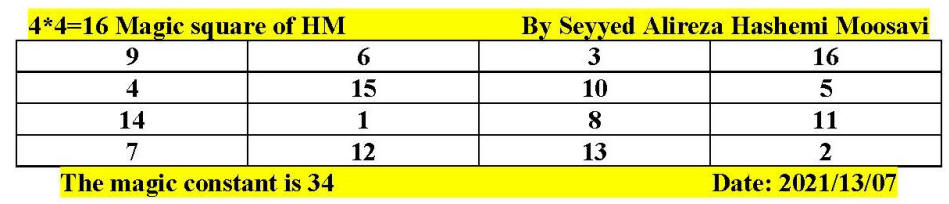
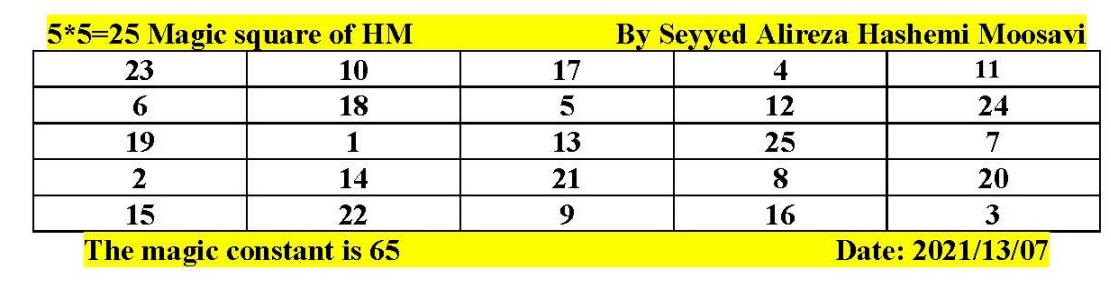
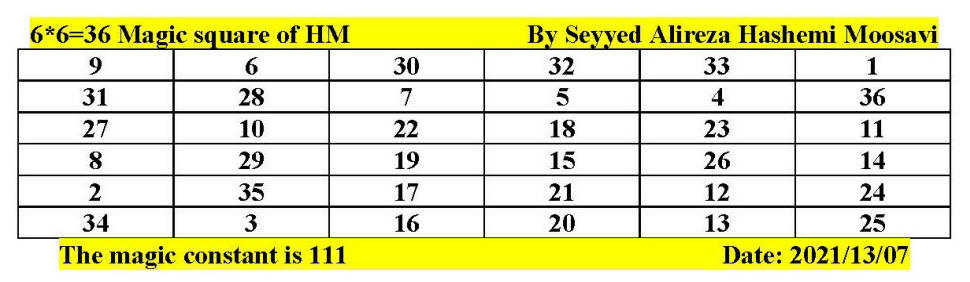
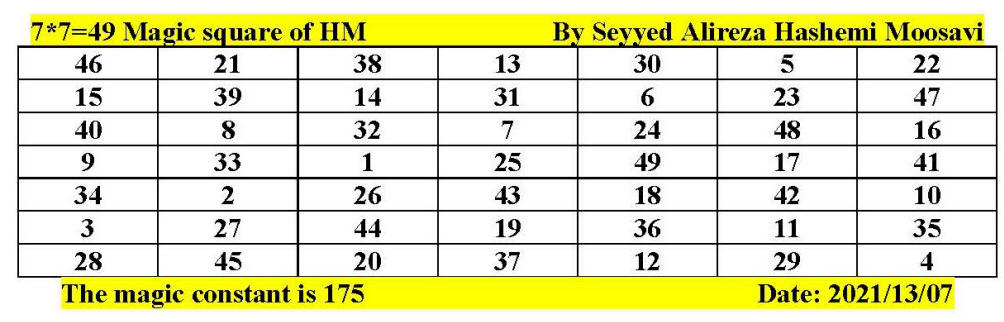
 Issue:  How can we determine large and very large primes?

This question on how to determine large and very large primes are most likely asked by most mathematicians, mathematics enthusiasts and students. Even long long time ago, the search for large primes was a focus of study and research. Fortunately, the people in the "gone but not forgotten" era came up with theorems, algorithms and formulas in getting these primes to satisfy the need. Among the contributors were Euclid who developed the Euclidian algorithm, Father Mersenne with his famous Mersenne primes, Eratosthenes with his Sieves of Eratosthenes, Fermat with his Factorization Method and Little Theorem and others like, Gauss, Riemann and Euler who belong to the antique generation. Further studies were also been conducted by enthusiasts in the middle ages and they came up to determine large primes without the help of a computer and mostly, done with their bare hands. To name few of them, they are Anton Felkel, J.P. Kulik, EDF Missal, BK Parody, J.R. Smith and S. Zarantonello, they are the ones who used to publish tables of primes in large numbers as we say it. Most of their work were based on the theorems and correlations from the prototypes of antique generation.

 So, what is the formula to determine exact large or very large primes? The answer is that based on the study, the accurate, exact and realistic method of determining large primes is by the use of Sieves of Eratosthenes. From the name itself you can think that numbers in a range are being sieved or "filtered" and that you can come up with real and exact primes. Here is an example of primes determined by the method in a range less than 100 or 10^2:   2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97....

Of course, the only problem with this method is that this is very tedious when done by hands especially when expanding in the range to 10^3, 10^4, or 10^n, where: n may be any number greater than 2. However, with the advent of computers, large primes may be generated with the Sieve of Eratosthenes faster than any publishable table may be read (Anderson and Bell, 1997, p.116). This is done by writing a program usually in high level computer language like Turbo Pascal or Turbo C using syntax such as arrays and loops that would command the computer to generate large or very large primes to a certain range. (Note: I am sorry that I could not discuss the programming technique here but I could give the key points in making a flowchart for this program)

The second question one might ask is: What is the use of other theorems or formulas made by Mersenne, Fermat or Gauss in determining large primes? 

The answer to that is the theorems or formulas made by these mathematicians were simple assumptions or estimations to get large primes and may or may not be representing exact single large primes. Let us take the definition of Mersenne which states that a Mersenne number is an integer of the form M (n) = 2^n - 1. If a Mersenne number is prime, it is called a Mersenne prime or can be stated this way "If  M (n) is prime, then n is a prime." Let us therefore prove if this is absolute.
 

Proof:

n             2^n - 1  =  M (n)                            Remarks

1             2^1 - 1  =  1                                    Empty

2            2^2 - 1  =  3                                    2 is prime; M (n) = 3 prime 

3            2^3 - 1  =  7                                    3 is prime; M (n) = 7 prime

4            2^4 - 1  =  15 = 3 x 5                     4 is not prime; M (n) = 15 composite

5            2^5 - 1  =  31                                  5 is prime; M (n) = 31 prime

6            2^6 - 1  =  63 = 3^2 x 7                6 is not prime; M (n) = 63 composite

7            2^7 - 1  =  127                                7 is prime; so M (n) = 127  prime

8            2^8 - 1  =  255 = 3 x 5 x 17          8 is not prime; M (n) = 255 composite

9            2^9 - 1  =  511 = 7 x 73                 9 is not prime; M (n) = 511 composite

10          2^10 - 1 = 1023 = 3 x 11 x 31    10 is not prime; M (n) =1023 composite

11          2^11 - 1 = 2047 = 23 x 89           11 is prime; M (n) = 2047 composite ?


As you can see in the table above, when n = 11; M (n) = 2047 = 23 x 89 which does not produce a single prime but rather composite. Therefore, we can deduce that Mersenne formula is good only for assumption for predicting primes but does not determine exact single large prime. The same thing also happens when we use Fermat number which is defined as a Fermat number is an integer of the form F (n) = 2^2n + 1. If a Fermat number is prime, it is called a prime. Unfortunately, the Fermat number, F(5) = 4294967297 is divisible by 641 and therefore, not a prime number and so Fermat number is also not absolute.
The third question one might ask is: Can we assume for a large prime number using the definitions or theorems made by antique mathematicians? 

My answer is yes. We could use the ancient formulas to predict or test a certain large number if its a prime or composite. The method is simple you just assume a large or very large number and test it for primality test. This is done using the theorem that if the positive integer n is a composite integer, then n has a prime factor p such that p^2 < n. This is also similar with the suggestion made by Dr. Wilkinson in his conversation with Mr. Ulric Cajuste ([usepmat_group]primes,1/16/10). Let us take a proof on this: ex. determine whether  n = 521 is prime?


Proof:

We only need to consider primes p that are less than or equal to 2 for 22^2 = 484 which is less than 521 according to the theorem p^2 < n. If we are to use 23^2 = 529 this would be greater than 521 and therefore, does not conform to the theorem. Hence, we have to use 22. The primes less than 22 or equal to 22 are 2, 3, 5, 7, 11, 13, 17, and 19. Trying these primes to be divided to 521, we find that none of the primes divides 521. Therefore, we can say the 521 is a prime. The only disadvantage with this method is that we just have to keep on guessing numbers until we find numbers to be prime.

Is there another formula aside from Sieves of Eratosthenes that could generate large primes? Yes, I have found one but this is subject yet to scrutiny. The equation looks like this:

P (n) = (2n + 1 - p) d N (n) + p = p (2n + 1 / p)^ d N (n)

where: N if N = 2n + 1 is prime

           p if N = 2n + 1 is composite (p: arbitrary prime number)


This equation was formulated by Prof. S.M.R. Hashemi Moosavi who claimed that he solved the problem on prime number generation. To prove this formula would be for our next discussion.

What is the rationale behind why computer companies offer prices to those who can get larger primes? I believe that the rationale behind offering prices by computer companies is that 1.) as a sort of advertisement 2.) to test their product, say computer. I am convinced that the greater weight falls to the second reason since computer companies tend to test their hardware such as processors or chipsets if it can perform long and complex mathematical operations, including also is the speed and time to process instructions. If you have comments about my reaction on this topic. Please feel free to write me or post a comment.


References:

James A. Anderson and James M Bell, Number Theory with Applications, 1997, Prentice Hall Publishing.

Prof. S.M.R. Hashemi Moosavi, The Discovery of on-to generating function of the prime numbers and its results. (www.primenumbersformula.com)

Date accessed: January 17, 2010.

 Ultima_syd, [usepmat_group] primes, 1/16/2010.


 horizontal rule

The Purpose Of Doubt In Knowledge Philosophy Essay

Info: 1284 words (5 pages) Essay
 Published: 1st Jan 2015 in Philosophy

The more I know about knowledge, then the more doubt will develop into my mind. That is what I felt about doubt through experiences in my life. We usually have doubt when we find it hard to belief our accept something as the truth. Doubts exist when our mind is in process of accessing something whether to belief or not to believe. When we are 100% confident about something that we think is true, then we will never misunderstood the idea that had been brought in the first place. Maybe without doubt, we would never come across the word “evolution” because evolution is about some facts that are due to the feeling of doubt. Key is something that can bring us nearer to the truth and as generator to the knowledge that we seek for. Doubt will lead us to find two form of knowledge.

 First is the doubt in knowledge which can help us to get clearer knowledge when we try to prove the claim made is true or not, second is the doubt in knowledge will lead us to discover and explore a new knowledge. Persian proverb says that “doubt is the key to knowledge” because from doubt, we have the feeling to know about something and perhaps will lead us to get clearer knowledge or new knowledge. We need to fulfill certain criteria before we can acknowledge something as a knowledge, such as it must be justified by empirical evidence, logic, memory or public authority. Without this criteria, a claimed knowledge made by scientist or historian can be myth. History and Mathematics are two different area of knowledge that can help us to find at what extent doubt is used as an element to discover new knowledge.

History is a subjective parts of area of knowledge and its talks about people and events of the past. It is not just the compilation of the past that is being recorded solely without any research and discussion, but after the facts are being interpreted and analyzed into something significant. Lets take an example of a history about Piltdown man. For instance, in 1912, a pale anthropologist, Charles Dawson claimed he have found human skull in England belong human ancestor aged about 500 thousand years ago or known as Dawson’s down-man. According to him, it is a pioneer evidence of human evolution. Most experts agreed that these specimens age about 500 thousand years old and being displayed in museums for more than 40 years. But out of sudden a few scientist doubt about the specimens was from human ancestor because the skull fragment and the jawbone obviously from two difference species. A few attempts were made by scientists to prove this claim was wrong but they did not succeed.

 Later, because of the advance in technology, a paleontologist, Kenneth Oakley has tried the technology of fluorine testing on Piltdown man in order to determine the actual age of the fossils. He applied the technology on the fossil and he found that the fossil is just a few thousand years not 500 thousand years as claimed by Dawson. Further investigation was made and it is found that the fossil is combination of human skull and ape. A conclusion is made by paleontologists that Piltdown man is a join together of a piece of jigsaw puzzle with the right color but wrong shape and was immediately removed from the museum. Piltdown man is an example that shows us that doubt can lead to get a clearer knowledge and can bring us and nearer to the truth. In order to agree the knowledge in history can be gained because of doubt, we have to realize that it has it own limitation and weakness. The weakness is doubts solely cannot solve any puzzles that we are wonder about. It must be accompanied by scientific method. The scientific method itself still can be doubted because human who created method can still make mistake. Maybe in the next few years someone will discover that fluorine technique used to investigate the date of the fossil is not accurate and valid enough to test for age of the specimens. We have to be remembered that science always evolve as time passes by and it is not impossible that more advance techniques will be discovered until the actual date and time the fossil belong to can be revealed. Henry Fairfield Osborn said that “We have to be reminded over and over again that Nature is full of paradoxes”. His statement is made to remind people that those things that we see and expect in this world does not necessary true as a lot more thing we don’t know about nature and the most important thing is we did not exist at the time of the history real event mentioned. Sometimes, historian only made a speculation or lucky guess on the specimens they found as long as it met their theoretical expectations. So it can be understood that even an evolutionist will get the closest interpretation on the fossil findings when they doubt and willing to discuss among themselves.

In other area of knowledge such as Mathematics doubt is still exist but in different view and perspective. This is because Mathematics differs from history in a way that it is more to objective, less ambiguous, less open to interpretation and more clearly defined. Math is more to numbers and can be differentiate very clearly which one is wrong and which one is right or in other word the answer is not subjective. Mathematics knowledge arises from problems that we face everyday and the solution in Mathematics is free from both observation and induction. In mathematics, people not always doubt whether the knowledge claim by mathematician is true or not because mathematics have the ability of self-proving and its objectivity, but people do doubt whether the claim made by mathematician about certain theorem can be modified in order to form a more perfect theorem. The simplest example is prime number formula. The definition of prime number is the number which can divide by 1 and itself.

As a student, I have doubt why number 1 did not count as prime number while number 1 can be divided by 1 and itself. But for mathematicians, they doubt whether prime number have a formula so that it can cover all prime numbers until infinity. After fail to solve this problem, Mathematicians claim that this problem is unsolvable. This unsolvable problem remains for 2300 years. Although this problem remains unsolved for so long, that doest mean mathematician had give up. The doubt grows deeper until in year 2003, Professor S.M.R Hashemi Moosavi found the formula for prime number. This shows that from doubt that prime number formula is unsolved we now can enjoy the fruitful of the doubt although it takes decades or centuries.

However, no ones would know that claim made by Professor S.M.R Hashemi Moosavi is the most perfect one to suit the formula for prime number because at this time no one can prove his theorem is wrong. Unlike the previous Mathematician, they also once had claimed that they have found this formula, but it only last for a certain period because someone had proven it only applicable up to certain numbers, not included until the infinity. We also can doubt what the last number of prime number is since the ending of infinity itself is unknown . Having discussed doubt is the key to knowledge from the perspective of two areas of knowledge namely history and mathematics makes me realized that doubt do exist in the process of searching for knowledge. Although the process obtaining knowledge though the feeling of doubt is differ in History and Mathematics due to its subjectivity objectivity and its nature, the final ending will bring us to only one destination; gaining knowledge. Therefore, doubt is the key to knowledge is agreed in these two areas of knowledge.

Reference : Ukessay. (November 2018). The Purpose Of Doubt In Knowledge Philosophy Essay. Retrieved from https://www.ukessays.com/essays/ philosophy/the-purpose-of-doubt-in-knowledge-philosophy-essay.php?vref=1

horizontal rule

Click here to see Introduction to Elliptic Curves

&

      New Proof of Fermat's last Theorem in 3 Different Way by HM Final Main Theorem

   horizontal rule

Magic squares            By Seyyed Alireza Hashemi Moosavi              date: 2021/13/07

 

 

 

 

 

 

 

 

 

 

 

horizontal rule

Why do people find these primes? 

 

 

"Why?" we are often asked, "why would anyone want to find a prime that big?""  I often now answer with "did you ever collect anything?"" or "did you ever try to win a competition?"" Much of the answer for why we collect large primes is the same as why we might collect other rare items. Below I will present a more complete answer divided into several parts.

  1. Tradition!

   2. For the by-products of the quest

   3. People collect rare and beautiful items

   4. For the glory!

   5. To test the hardware

   6. To learn more about their distribution

This does not exhaust the list of reasons, for example some might be motivated by primary research or a need for publication. Many others just hate to see a good machine wasting cycles (sitting idle or running an inane screen saver). Perhaps these arguments will not convince you. If not, just recall that the eye may not see what the ear hears, but that does not reduce the value of sound. There are always melodies beyond our grasp.

  1. Tradition!

Euclid may have been the first to define primality in his Elements approximately 300 BC. His goal was to characterize the even perfect numbers (numbers like 6 and 28 who are equal to the sum of their aliquot divisors: 6 = 1+2+3, 28=1+2+4+7+14). He realized that the even perfect numbers (no odd perfect numbers are known) are all closely related to the primes of the form 2p-1 for some primes  p (now we call them Mersenne). Large primes (especially of this form) were then studied (in chronological order) by Cataldi, Descartes, Fermat, Mersenne, Frenicle, Leibniz, Euler, Landry, Lucas, Catalan, Sylvester, Cunningham, Pepin and Putnam . How can we resist joining such an illustrious group? Much of elementary number theory was developed while deciding how to handle large numbers, how to characterize their factors and discover those which are prime. In short, the tradition of seeking large primes (Especially the Mersenne) has been long and fruitful It is a tradition well worth continuing.

  2. For the by-products of the quest

Being the first to put a man on the moon had great political value for the United States of America, but what was perhaps of the most lasting value to the society was the by-products of the race. By-products such as the new technologies and materials that were developed for the race that are now common everyday items, and the improvements to education's infrastructure that led many man and women into productive lives as scientists and engineers. The same is true for the quest for record primes. In the tradition section above I listed some of the giants who were in the search (such as Euclid, Euler and Fermat). They left in their wake some of the greatest theorems of elementary number theory (such as Fermat's little theorem and quadratic reciprocity).  More recently, the search has demanded new and faster ways of multiplying large integers. In 1968 Strassen discovered how to multiply quickly using Fast Fourier Transforms. He and Schönhage refined and published the method in 1971. GIMPS now uses an improved version of their algorithm developed by the long time Mersenne searcher Richard Crandall .The Mersenne search is also used by school teachers to involve their students in mathematical research, and perhaps to excite them into careers in science or engineering. And these are just a few of the by-products of the search.

  3. People collect rare and beautiful items

Mersenne primes, which are usually the largest known primes, are both rare and beautiful.  Since Euclid initiated the search for and study of Mersenne approximately 300 BC, very few have been found. Just 37 in all of human history--that is rare! But they are also beautiful. Mathematics, like all fields of study, has a definite notion of beauty. What qualities are perceived as beautiful in mathematics? We look for  proofs that  are short, concise, clear, and if possible that combine previous disparate concepts or teach you something new. Mersenne have one of the simplest possible forms for primes, 2n-1. The proof of their primality has an elegant simplicity. Mersenne are beautiful and have some surprising applications.

  4. For the glory!

Why do athletes try to run faster than anyone else, jump higher, throw a javelin further?  Is it because they use the skills of javelin throwing in their jobs?  Not likely.  More probably it is the desire to compete (and to win!) This desire to compete is not always directed against other humans.  Rock climbers may see a cliff as a challenge. Mountain climbers can not resist certain mountains. Look at the incredible size of these giant primes! Those who found them are like the athletes in that they outran their competition. They are like the mountain climbers in that they have scaled to new heights. Their greatest contribution to mankind is not merely pragmatic, it is to the curiosity and spirit of man.  If we lose the desire to do better, will we still be complete?

  5. To test the hardware

Since the dawn of electronic computing, programs for finding primes have been used as a test of the hardware. For example, software routines from the GIMPS project were used by Intel to test Pentium II and Pentium Pro chips before they were shipped. So a great many of the readers of this page have directly benefited from the search for Mersenne. Slowinski, who has help find more Mersenne than before, works for Cray Research and they use his program as a hardware test. The infamous Pentium bug was found in a related effort as Thomas Nicely was calculating the twin prime constant. Why are prime programs used this way? They are intensely CPU and bus bound. They are relatively short, give an easily checked answer (when run on a known prime they should output true after their billions of calculations). They can easily be run in the background while other "more important" tasks run, and they are usually easy to stop and restart.

  6. To learn more about their distribution

Though mathematics is not an experimental science, we often look for examples to test conjectures (which we hope to then prove). As the number of examples increase, so does (in a sense) our understanding of the distribution.

horizontal rule

Breaking the code - How to determine large and very large Primes?

A discussion on how to determine large and very large primes from the context of

 Number Theory

          Monday, January 25, 2010

Breaking the code - The Moosavi Formula

 

Breaking the code - The Moosavi Formula


I have found the formula to determine the prime at the k-th level. This formula is named as Moosavi formula formulated by Prof. S.M.R Hashemi Moosavi. I would say that this is the final formula that unveils the mystery of primes. You will no longer need a computer to determine the prime at the k-th level if you can do it by hands. Here's  the list:
 


Reference: 

www.primenumbersformula.com

 

Posted by at  

horizontal rule

Breaking the Code Part 2 - Which is which? The Sieve Algorithms

or The Primality Test Equations

Issue: Breaking the Code Part 2 -Which is which? The Sieve Algorithms or The Primality Test Equations 
 

Yes, I agree with Mr. Jay that the modern sieve of At kin is more complicated, but faster when properly optimized.[1] At kin's algorithm is actually more efficient than the sieve of Eratosthenes when run in computers. This is somehow due to the fact the algorithm takes less memory of the computer than its predecessor the sieve of Eratosthenes. This can be proven by the statement from Wikipedia that the At kin sieve computes primes up to N using O (N/log log N) operations with only N1/2 + o(1) bits of memory. That is a little better than the sieve of Eratosthenes which uses O (N) operations and O(N1/2(log log N)/log N) bits of memory[2]. However, this does not amplify so much for there is only minor advantage when both are compared. But, what I am quite unsure of, is the findings of my pal that the sieve of Eratosthenes is useful only for relatively small primes.[3]Before we further our discussion, friends, may I know your opinions on the following questions:
 

1. "Which is better?" - Which do you think is better in finding the large or very large primes: The algorithm method? or Is it the use of primality test equations? 

2. "How large is your large?" - How large is your large prime that you think this is the largest prime? 

3. "How fast are you?" - Which do you is more faster, the manual method or the computer generated method of locating prime? If you have comments about my reaction on this topic. Please feel free to write me or post a comment in this site.

References:
 Jay08_20, [usepmat_group] primes, 1/19/2010   [1], [3]
http://en.wikipedia.org/wiki/Sieve_of_Atkin, (Date accessed: 01/19/2010)   [2]
http://stackoverflow.com/questions/622/most-efficient-code-for-the-first-10000-prime-numbers

 

horizontal rule

Click the link to download or open the PDF file of New Proof of Fermat's last Theorem

by Final - Main HM Theorem

horizontal rulehorizontal rule

 

Download The PDF File Of Primality Test

https://studylib.es/doc/5773406/resumen-desarrollo-del-proceso-de-producción-de

horizontal rule

 

 

horizontal rule

Home | Contents of The Book | About Me | Article | Books | Photo Gallery | Contact

horizontal rule

This site was last updated 06/27/23 19:14:11 +0330