CHAPTER 1

A brief of view of number theory

1.1. Number theory in ancient time

We should have a quick review to the past (before Fermat in 17^th century). Mesopotamia civilization (2000-3000 B.C) is the first civilization, which presents documents that indicate mathematical activities at that time. At that time there was not paper and the process of writing has been done on the tablets which made of clay with a kind of hard writing that called cuneiform; there are calendars which the history determines the beginning of this are about 2000 B.C and it shows that Summer ions had an understanding of topologic measurements, simple and complex interest, the solution of the square equations and their uses of negative numbers. The first convincing sign which archeologist scientists found was in 1945 and it was the time that A. Negiver and A. Sakhz analyzed a table which was known to Plimpton 322 (Plimpton library from Colombia University). From the language that used in it, we can comprehend the history of it a little closer at 1600-1900 B.C. However there is a schedule in it including 15 answers for equation  which from difficulty point they are (3,4,5) to (12709,13500,18541).

In addition, the sequence of numbers have been written in a special way, indeed, it is requested to reduce an angle of a right triangle with (x, y, z) sides from 45^o to 31^o. Evidently, Babylonians knew not only Pythagoras theorem and eventually the sense of trigonometric functions, but they use a rule for finding the answers of Pythagoras equation. If we suppose that all of these are not extraordinary enough, we should say these people have done all of these acts without symbolic algebra and without sense of common demonstration. It does not seem that Egypt mathematics that has remained on the parchment wholly shows the proceeding of Mesopotamia in mathematics. The obtained works from B.C. Indo china are very scattered but the important thing is that the acts which were done in Indo china have not had any effect on the development of numbers theory. The subjects which are known as mathematics today like deduction, proof and theorem, started from Greeks. Probably conclusion has been used by Tales (548-624 B.C) and almost was used by the students of Pythagoras school.

Pythagoras (500-580 B.C) traveled to Babylon, Egypt and probably India. He was philosopher and Gnostic, gave importance of counting and philosophy. Probably he and his followers were depended on the senses of pictorial number (triangles numbers 1, 3, 5, 10,…; square numbers, etc), perfect numbers (for example, 28 is a perfect number because it is equal to 1+2+4+7+14, the sum of its divisors less than itself), amicable numbers (for example 220, 284 because each of them equals to sum of another real divisors). But, it is not obvious which one of them had proved theorems in these cases. About 300 years B.C. the first institute like university witch was called "museum" established in Alexandria and its first scientific member was Euclid. However, Euclid was a famous mathematician, most of the subjects that he reviewed in "principles" book, has been formers works.

The volumes number IX, VIII and VII of principles book has appropriated to number theory. Unique decomposition theorem equals with theorem 14 of IX book. The existence of infinite numbers of prime number is 20^th theorem of IX book.

Among three famous mathematician that created the golden era of Greek mathematics (200-300 B.C). Euclid, Archimedes, Apollonius he is only Euclid that seems to had done much researches in number theory. At most time, mechanics and geometry were paid more attention to it and it took time more than 3 centuries to Diophantus an Alexandrian Began a new way with his outstanding work "arithmetic". In his about 13 volumes treasure that has remained just 6 volumes of them, an other has started multi variables (unknown) equations, Equations with two or more unknown quantity which answers belong to Q⁺ or (today) to Z. Also, these books include some theorems such if two integer numbers which each of them equals to the sum of two squares that the product of them is also equals to the sum of two squares. According to indirect evidences, it seems that Chinese have known much mathematical subjects before finding out them in else whereas which include Pascal’s triangle and simple magic squares. On other side, probably because they had no relation to others, their portion in mathematics is considered just in "Chinese remainder theorem" that its date, is some centuries ago.

In India, Brahmagopta discovered general integer answer of linear Diophantus equation" ax+by=c".

But Diophantus had verified only equations with higher degree, because linear equations are obvious when rational answers were considered. And always he binds himself to special and singular answers. Some years later Bascara (1114-1185), solve equation  in especial cases (many years before that, samples of this equation was solved by Archimedes or one of his contemporaries and also by Diophantus).

With decreasing the influence of Greeks, and then advent of roman imperial
(that had not present a new thing in mathematics), center of civilization was transferred to Baghdad. Probably Harmonious Knowledge of Babylonians, Egyptians, Greeks and Hindus were useful but less than was expected.

1.2. What is number theory?

This question is motive of primary attempts to present a definition. Number theory is the study of set of integer numbers or some of subsets of it or sets include it, with this thesis that integer numbers are interesting alone and in relative to each other, without attention to their useful role in measurement. Apparently, domain of this definition include primary arithmetic that infect, it is in this manner except cases about exact and improvement aspect.

We return to 17-century, for taking an idea and knowing what we will speak about the time that Pier Fermat’s[1] work started a new era in mathematics. One of the most beautiful Fermat’s theorems is that every positive integer number can be shown as sum of squares of four integer numbers. For example:

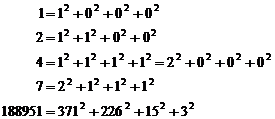
(According to this point, multiplication of two representable numbers is a representable number; it is enough to prove that every prime number "P" is representable).

He propounded this theorem in 1636, but the first printed proof of it, presented in 1770 by Joseph Luis Lagrange. This theorem has an ideal aspect in theorems of number theory that is: beautifully, understandable fast, reveal and exact and unexpected relation between integer numbers, the best result in relative to its
kind (7 cannot be shown as sum of less number than squares) and it is a proposition about infinite set of integer numbers. The last one is very important, because it determines difference between theorems and numeral truth. This subject that 1729 is the smallest positive integer number that has two representation as sum of two cubes is true and probably is one of interesting truth, but we can’t named this truth as a theorem. Because it can be proved by testing finite set
1, 2, …, 1729.

In other side, we consider the proposition "only finite integer numbers that exist have. Two or more presentations of that kind" is seducer. It seems that this proposition express a subject about finite set, but in fact, we can not prove or reject every finite set with testing. Therefore, this proposition will be an important theorem if it is true (Of course always isn’t true).

Another more famous subject that is attributed to Fermat and sometimes called his latest theorem, expresses that if "n" be an integer number greater than "2", the equation  has not answer in positive integer numbers set. Fermat claimed that he proved this but as his habit, he did not express its proof. It seems, this, is only recorded example that he claimed a result which he never proved it (Although he propounded a false guess about the prime number  that we will express below). Because of lacking any demonstration for this claim, modern mathematicians prefer that called it Fermat’s problem instead of Fermat’s theorem. This is the oldest and maybe the famous unsolved problem in mathematics. Although only a counter example is enough to discredit it, but finding four numbers x, y, z and "n", if they exist, is out of capacity of future and now a day computers. Because, now, it is clear by to calculate that this equation has not answer for  and if answer exists, one of x, y or z must be greater than .

(The known worlds can contain only  objects in proton size).

One of the basic concepts of number theory is prime numbers. Integer number "p" is prime if  and equation  has not answer with respect to integer number "a" and "b", except or. Therefore, we can say briefly that a prime number is an integer number that is opposite of  and has not any non–trivial divisor. Before, Euclid knew that sequence of prime numbers 2, 3, 5, 7, … doesn’t finish and manner of their appearance is very irregular. Fermat and Mersenne also were seeking a kind of order and both of them guessed a wrong thing. Fermat guessed that all of numbers are prime numbers that in fact, this conjecture is true for n=0, 1, 2, 3, 4. After sometimes it clarified that it stops soon, because Leonard Euler in 1739 showed that "F₅" is a divisor of "641". In fact, for  any prime value didn’t find for F_n. Since false guesses about prime numbers are very frequent this story wouldn’t (be) very valuable if Fermat’s prime numbers appears "200" years later in different situation again. Carl Fredrich Guass[2] searched one of ancient Greece’s problems. He proved that regular m-angle can be made by ruler and compass if and only if (IFF) "m" can be factorization in form, that k,n₁,…n_r are non-negative integer numbers and are Fermat’s distinct prime numbers. So it is interesting to know whether prime numbers more than this kind exist or not?

Although portion of Mersenne in Mathematics was propagating the new results more than creating them, but he studied prime numbers among numbers in form.

If , then "M_n" is divisible by "M_r" and also by "M_s". Therefore "M_n" can be prime Just for prime values of "n". In 1644, Mersenne expressed that from "55" numbers of "M_p" that, the ones which are prime number, are corresponding with . So, Mersenne committed "5" errors. Because he took into account 67 and 257 and he didn’t teak into account 61, 89 and 107. It isn’t attention able that he had wrong but it is important that he could gain information about numbers which have 78 digits without pocket calculator. Again we see numeral truth, not theorem, and frankly some cases must be hidden beyond these subjects, that "N is prime number if …" or "N isn’t prime number if …" and such cases are useful. Always there is strong interaction effect between intuitive truth and theorems of numbers theory. Calculations give information that we can infer from them some counter examples or theorem’s guesses and also subjects for useful theorems which lead to useful algorithms. (Algorithm means methods for calculation).

Fermat's numbers and Mersenne's numbers are so scattered that if all of them be prime numbers, we can infer a little information about distribution of prime numbers in them.

Other useful and prominent studying by Guass was started in 1792 by using a table of prime numbers smaller than 102,000 that some years ago printed by John Lambert. If as it is usual,  was indicator of the number of positive prime numbers not more than "x", then what Guass did, was searching the increments of  according to the increments of "x". He started by enumeration of prime numbers in intervals with constant lengths and obtained a table like below, in which:

Average of the number of prime numbers reduces in successive interval and Guass chose inverse of  and compared it with different primary function. Below table is obtained about natural logarithm of "x":

X	1000	2000	3000	4000	5000	6000	7000	8000	9000	10,000
	0.168	0.135	0.127	0.120	0.119	0.114	0.117	0.107	0.110	0.112
	0.145	0.132	0.125	0.121	0.117	0.115	0.113	0.111	0.110	0.109

Wonderful match of these numbers strengthen, this guess that  is almost equal to . Since  is equal to slope angle of a segment on curve  we must integrate the approximate equation of  so that  can be calculated, therefore Guass guessed:

This Integral isn’t a primary function and usually is shown by . Its values are calculated easily and modern calculations present the below comparison (that is given with its nearest integer number)

10^3	168	178	10	0.94382
10^4	1,229	1,246	17	0.98636
10^5	9,592	9,630	38	0.99605
10^6	78,498	78,628	130	0.99835
10^7	664,579	664,918	339	0.99949
10^8	5,761,455	5,762,209	754	0.99987
10^9	50,847,534	50,849,235	1701	0.99997
10^10	455,052,512	445,055,614	3102	0.99999

What Gauss expressed in present ion a guess that  is a good approximation of  for great "x", wasn’t that, or even  is limit, but this was that its relative error is little:

Or:

                 (1)

He guessed this subject in 1793 when he was "15" years old. But this subject wasn’t proved, till more than "100" years later Hadamard and Poisson proved it (independently in 1896). Its demonstration is too hard that can be expressed in this book. But it is possible to show that if limit of (1) exists, its value is equal to "1".
It is not so difficult to show (1) result:

             (2)

This subject and its inverse are proved. Because of Basic situation that relation (1) or its formal form (2), have in number theory, it is known as "theorem of prime numbers".

Reason for studding the information of latest table for great number of "x" which Gauss didn’t calculate  for them, it is that persists on this important point that never calculations  can substitute instead of demonstration. As the table clearly shows that always present with abundant approximate. It means that at least value of [] is positive and increasing to. But this isn’t permanent, because Littlewood in 1914 showed that the sign of [] changes infinite times. No body knows that when first sign changing occurs. But Skewes in 1955 proved that this subject happens for "x" that. Probably no determinate value will be found for "x" in future so that for it. Many questions exist about prime numbers that all of them remain unsolved in front of attempting in two century or more, for example, is there infinite number of twin prime numbers like 17 and 19, 4967 and 4969 so that their difference is "2", and is every even number greater than 4 equals to sum of two odd prime numbers?

Now, for variety we express a question that has less celebrity and hasn’t been propounded recently and it seems be very hard. We form below double infinite array that first row include prime numbers and every number of below rows equal to absolute value of subtraction of its two upper numbers. Is it true that every row except the first row starts by "1"? This subject is true about a part of array that is written in below up to p=53 and it is justified up to p=792721. There are some branches of number theory that integer numbers exist in them less then the prime number theory.

2		3		5		7		11		13		17		19		23		29		31		37		41		43		47		53
	1		2		2		4		2		4		2		4		6		2		6		4		2		4		6
		1		0		2		2		2		2		2		2		4		4		2		2		2		2
			1		2		0		0		0		0		0		2		0		2		0		0		0
				1		2		0		0		0		0		2		2		2		2		0		0
					1		2		0		0		0		2		0		0		0		2		0
						1		2		0		0		2		2		0		0		2		2
							1		2		0		2		0		2		0		2		0
								1		2		2		2		2		2		2		2
									1		0		0		0		0		0		0
										1		0		0		0		0		0

For example, in problems about nature of numbers like "" and "e", such a situation exists. This question that whether every one of these numbers are rational or not, in fact is equivalent that whether every one of them is an answer for a linear equation like  with correct coefficient or not? Lambert[3] Switzer mathematician, mentioned before that and later in 1761 proved that  isn’t a rational number. Generally, this question can be propounded that, are "e" and  algebraic or not? In other word, are any of them adapted in a polynomial like  with integer coefficient like  or not?

Again in both cases, it is proved that answer is negative but their demonstrations are a little hard. If we verify the problem on other side, we can study the numbers that are algebraic and therefore it seems that a strong theory can be built on it, so that it will be an interesting subject and a useful instrument to study the integer numbers.

1.3. Prime numbers

In this book, we consider on positive divisor of numbers. Therefore, we speak about "divisor", it means positive divisors unless against of this mater is emphasized. For example the only divisors of 6 are 1,2,3,6.

1.3.1. Definition

Natural number "" is prime when its divisors are only "1" and "p". Each natural number except "1" is compound when isn’t prime. From this definition, it results that "1" is neither prime nor composite. Also natural number like "n" is a composite number if and only if  that . The prime numbers less than "100" are written in Pythagorean’s table:

2,3,5,7,11,13,17,19,23,29,…,97

Since the only positive divisors of prime number "p" are "1" and "p", then for each integer number like "a" we have ()=1 or , it means, "a" is
coprime with "p" or "p" aliquots it. Therefore, sometimes it is correct to write  instead of .

Now we suppose "p" is prime and "a" and "b" are two integer numbers so that . If , then  and it results . Therefore, the products of two integer numbers are divisible by prime number "p", if only at least one of those two numbers be divisible by "p". This result can be extended to multiplication of a finite number of integer numbers. Using product symbol  , we show following General result.

1.3.2. Lemma

Consider "p" is prime number and "k" is natural number. If  be integer numbers so that  then for one "i",  we will have . Now we express and prove the following lemma.

1.3.3. Lemma

Each natural number  has a prime factor.

Proof. Suppose that  is a supposed natural number and "S" is set of all divisors of "n" greater than "1". Since , than the set "S" is non-null and consequently "S" has a smallest member, namely "p". We prove that "p" is prime number. Since each divisor of "p", is a divisor of "n", therefore if "p" is composite then it is  necessary that "S" has a member which is less than "p" and this is impossible, therefore "p" is prime. The following theorem is from Ecocides and therefore this theorem is over 2000 years old.

1.3.4. Theorem

The number of prime numbers is infinite.

This theorem means that if we suppose each natural number like "n", the number of prime numbers is more than "n". We suppose  are "n" different prime numbers. We write. According to lemma (1.3.3), "N" has a prime factor like "p". In the other hand, no value of  is factor of "N", because in this conditions it is necessary that . Therefore "n+1", prime numbers  are distinct. So we could prove the theorem’s demonstration, by induction.

There are easy ways for classifying prime numbers. In the firs stage it seems that each natural number is either even or odd, it means that each number is in the form of "" or "" that "n" is non-zero integer number.

But "2n" can’t be prime except for "". Then each prime number is odd except 2. Therefore we could deform the above theorem that the number of odd prime numbers is infinite.

To this way, because reminder of division of each integer number by 3 is 0,1,2, then each natural number is in one of these three forms and "n" is a natural  number. Again "" can not be a prime number unless for n=1. Then each prime number except "3" is in form of or . In other word, every prim number except "3" is in form of . Therefore, the number of prime numbers is infinite to this form .

Now in the next step we remind that each natural number is in these forms  that "n" is natural number.

It is clear that "4n" isn’t prime never and is prime only for n=0. Then each odd prime number is in one of these form or . In the other hand, each odd prime number is in form. Therefore numbers of prime numbers which are in this form are infinite.

Also we can classify prime numbers according to residuals of dividing by each positive correct number and constant (as it used in 2, 3 and 4).

The following theorem is famous to Dirichlet, it is proved in some special condition with the elementary way, but we don’t know easy demonstration for general state of this theorem. Therefore, we express the theorem without proof. Its especial state is urgent result of theorem (1.3.4) for .

1.3.5. Theorem

 If "a" and "b" be two natural number and , then the number of prime numbers in "" form is infinite ("n" is the natural number).

1.4. The fundamental theorem and some of its applications

 In the some way we will show, it is completely clear that each correct number is  or prime or we can write it in a form like multiplication of prime numbers. According to lemma (1.3.3), number "a" has a prime factor like  and therefore there is a natural number like  in that .  So, there is a natural number like  in that  or . If  then "a" written to way as multiplication of the primes  and . Now, if  then  must have had a factor like  and . Since  so this sequence can’t repeat to extreme infinite times and we must have  for natural number like "r", and then . But it isn’t necessary that all of prime numbers  be different result. To this way we proved a part of the following theorem and this theorem has an important role in studding integer numbers which usually it is famous to Arithmetic basically theorem. Before speaking about the theorem we accept that there is a multiplication even with one factor. Therefore, it isn’t necessary that we express different theorem for the situation that "a" is prime itself.

1.4.1. Basic theorem

We can write each natural number  with only one way as multiplication of prime numbers (without attention to the order of factors). Part of the theorem proved above. Now we prove, showing each natural number is in form of multiplication of unique prime numbers. We suppose that it is possible to write "a" to two in different way as the form of multiplication of prime numbers, it means that  and  which "" and "" are prime And "" isn’t equal to "" exactly, Then we have:

Now, if we delete equal prime numbers from both side of equality, with again symbol:

That  and . It results and from lemma (1.3.2) it is necessary that  aliquot one of the prime numbers . Therefore  must be equal to one of "" that it is against of omit ion of equal prime numbers of both side of above equation. So this thesis is paradox that we can write "a" by two different methods as multiplication of prime numbers. So, proof of theorem becomes complete.

In writing of integer number , as multiplication of prime numbers, some times it is better to use symbol which show all of the different prime factor of "a". Previous theorem shows that we can write each natural number a>1, only by one way:

          (1)

That are the different prime factors of "a" and . The right side of equation (1) named form of standard factorization of integer number "a".

Now, we suppose  and (1) is standard factorization of "a". We suppose a=cd and ,. If we express each of "c" or "d" as multiplication of prime numbers (it isn’t necessary that all of them be different) and we put it instead of "c" and "d" in , then "a" will be written as multiplication of prime numbers. If we look at equal prime numbers together in this multiplication, then according to basic theorem (1.4.6), number "a" exactly is written as form (1). Therefore, we will have easy but important following theorem.

1.4.2. Theorem

If standard factorization of number "a" be in (1) form then the divisors of "a" are exactly numbers like "d" in following form:

       (2)

It is clear for number "a" we can give  with selection  in (2). Also with Selection  we can get "a" itself. Remember that no need that (2) be standard factorization of "d", because it is possible that some or all of the powers be zero. We can get the greatest common divisor and smallest common multiplication of two number a>1 and b>1 from the standard factorization of "a" and "b". For this, we change symbols a little. We suppose  are different prime factors of "a" or "b". Therefore:

  ,                  (3)

That "" and "" could be zero. Nevertheless, for each i=l, 2,…, t, at least one of "" or "" are greater than zero. We show the greatest and smallest number of  respectively by and.

It is clear that when  then , then with this expression, the following result is clear.

1.4.3. Theorem

 If "a" and "b" be in form of (3), then:

For example, we suppose that a=360 and b=126. Standard factorization of these integer numbers are  and

With use of theorem (1.4.3) we will have:

Now, for finding the number of one positive integer number’s divisors, we obtain an easy formula. For example, according to theorem (1.4.2), divisors of  are in  from that in which  is one of these four values 0,1,2,3 and  is one of these three numbers 0,1,2 and  is one of these two numbers 0,1. So,  selections exist for  and . Therefore, the number of divisors of 360 is .

Generally,  selections exist for  in (2) and so we can say:

Whenever (1) be standard factorization of number "a", then the number of divisors of "a" is in below form:

.

Also, we can gain a formula for calculating the sum of all of divisors of supposition integer number "a". Here we suppose the number  for clear expression. We can show that multiplication:

As sum of 24 terms in below form:

,  ,

In fact, above multiplication is equal to sum of all integer numbers in form , so that ,  and , namely equal to sum of divisors of number 360, because:

Therefore, sum of divisors of number 360 is:

.

1.4.4. Attention

Sometimes, it is better that we use symbol for the summation that domain of "d" is positive divisors of "a".

For example,  is sum of all divisors of "a".

It is interesting to remember that we can factorization all of the numbers smaller than , it means 10000 to multiplication of prime factors with knowing the prime numbers smaller than 100. We suppose "N" is a non–prime number and smaller than 10000, we have in this situation. In which "a" and "b" are prime or non-prime. If "a" and "b" are greater than 100, in this state, multiplication of "ab" will be greater than 10000 and contradict with this our supposition, since "N" is smaller than 10000. If for example "a" be a number smaller than 100, it means that there is a prime factor smaller than 100 (namely one of the 25 factors which are mentioned before). Therefore it is enough to know that the number "N" is divisible by which of these 25 numbers and if "N" isn’t divisible by any of them, it is prime number. For example we consider number 7458:

Number 1243 isn’t divisible by none of 7 or 5, but we have:

And we can’t continue the following action, because 113 is smaller than square of 11 and with paying attention to calculations that we have done, it isn’t divisible by any number smaller than 11 and therefore it is a prime number.

Then, we can be assured by a general method that "N" is prime number, when it isn’t divisible by any prime numbers smaller than "p". This method that is about primality of a simple special number, is very hard when it is used for the great number of numbers and it is obvious that it is impossible for millions numbers. There is an easy method for this case. It was very usual since many years ago. It is related to Eratosthene and in this method, we identify the non-prime numbers among the numbers smaller than 10000 or 100000 and etc, and then we determine the least divisor of them which is prime. This way is known as Eratosthene sieve.

1.5. Sieve of Eratosthense

Suppose that we want to determine the prime numbers smaller than 100. At first we omit even numbers, then we write the odd numbers on the consecutive rows (for example 10 number in each row), in this way we will have:

1	3	5	7	9	11	13	15	17	19
21	23	25	27	29	31	33	35	37	39
41	43	45	47	49	51	53	55	57	59
61	63	65	67	69	71	73	75	77	79
81	83	85	87	89	91	93	95	97	99

Then, before doing any work, we omit the multiples of 3 and this work is very easy, because these multiples are three-to-three.

When we omit the multiples of 3 no need to take into account the omitted even numbers, but after omitting the multiples of 3, if we want to omit the multiples of 5, we must consider the numbers five-to-five, without ignoring the multiples of 3 that have omitted them before.

For omitting the considering multiplication, it is better to adjust the above table to the following form, that in the two end of the rows there are decimal digits and in the top of columns, there are mono-digits.

	1	3	5	7	9	1	3	5	7	9
0					3			3			1
2	3		5	3			3	5		3	3
4			3		7	3		5	3		5
6		3	5		3			3	7		7
8	3		5	3		7	3	5		3	9

At first, we put the number 3 in the squares which adapt to numbers divisible by 3 (except the number 3 which is prime number). We will do this work for number 5 and then 7. Finally the squares which are empty show the prime numbers. It is clear that the numbers 3 has a regular order in this table, along some diagonals, there is the same order for numbers 5 and 7, especially if divisors of 5 and 7 exist in equerries that also divisors of 3 exist, this situation is more obvious.

1.6. Periodic sieve for small numbers

If we note that sieve has a certain period, especially for the smaller prime divisors, then a lot of calculations can be done easier. At first we pay attention to divisors of 2 and 3. The multiple of these two numbers are equal to 6 and it results that if a number is not divisible by 2 and 3 it will be in one of these forms:

           (1)

It means that in any successive 6 numbers, there are two numbers that they aren’t divisible by 2 and 3. Now we search for the numbers which are divisible by 2, 3 or 5. We can see, between these numbers, there are only three numbers 2, 3 and 5 which are prime. Nevertheless we consider them as the numbers which are divisible by 2, 3 or 5.

Between numbers of (1), which are divisible  neither by 2 nor by 3, we can obtain the numbers smaller than 30 for n=0,1,2,3,4 (for 5 values of "n"), In this way we will have  numbers. But among these numbers which aren’t divisible by 2 or 3, there are only two numbers which are divisible by 5. These two numbers come from the multiple of 5 by two numbers less than 6 (which are coprime with 2 and 3). Subsequently the number of numbers which aren’t divisible by any numbers 2 and 3 and 5, are equal to:

These 8 numbers are prime except "1":

Since the number 30 is divisible by 2 and 3 and 5, the numbers which are in one of the following forms:

aren’t divisible by 2 and 3 and 5. These numbers aren’t necessarily prime, but, we must look for the prime numbers among them. On the other hand, for a number to be prime, the condition (2) is necessary but not enough.

Now, we consider the prime number 7. The numbers smaller than or equal to multiple of , obtain from the relation (2) for seven values of "n", namely 0,1,2,3,4,5,6.

By this method we get  numbers which all of them are smaller than "210" and none of them are not divisible by 2, 3 or 5.

Among these numbers, how many of these numbers are divisible by "7"? If these numbers are divisible by 7, quotient is a number between "1" to "30" and because none of these numbers are divisible by 2 and 3 or 5, Therefore their quotient by 7 is a number not divisible by 2,3 or 5, subsequently this quotient is one of eight numbers which we mentioned them before. Conversely the multiple of each of these eight numbers by 7:

7,49,77,91,119,133,161,203          (3)

Will be the numbers smaller than "210" and not divisible by 2, 3 and 5, but they are divisible by 7. Finally among the first 210 numbers, the number of numbers which aren’t divisible by 2, 3, 5 and 7 will be:

These 48 numbers, numbers are which obtain from relation (2) for
n=0, 1, 2, 3, 4, 5, 6, as if we omit the mentioned numbers in relation (3).

If  is representative of every one of these 48 numbers, the numbers which are in this form:

        (4)

are not divisible by 2, 3, 5 and 7. Therefore they could be prime numbers. In fact, all 48 numbers aren’t prime and among them, there are numbers which aren’t prime:     

In this way, we can study the first 2310 numbers using the prime number "11" which is immediately after 7..

Among these numbers, these are  numbers[4] of , which none of them are divisible by 2, 3, 5, 7, 11 and they are written in this form[5]  and we must search for they prime number only between them. Now if we consider the prime number like 13 too, then we will obtain:

that its appearance form is also very simple. Among these 30030 primary numbers there are:

Number which aren’t divisible by any prime number smaller than 17. For obtaining the prime numbers smaller than 30030, we must omit the multiples of 17, 19, … up to 173 (square root of 30030) among them. This is relatively a detailed work, but since it omits  numbers which are divisible by one of these number 2, 3, 5, 7, 11 and 13; In the first step, it facilitate the job.

1.7. The infinity of prime numbers

From what is said up to now, we can result easily that the prime numbers sequence is infinity, or in other word the last prime number doesn’t exist.
In fact, by an easy calculation which has have done before , it is resulted that if we consider only the prime numbers 2, 3, 5, 7, among the first 210 numbers greater than "1", there are 48 numbers which we can’t obtain them by multiplication of one of these four prime factors by the others. If we consider more prime numbers, but restricted, there we will find more numbers which aren’t resulted from multiplication of these few prime numbers. For example if we consider the prime numbers 2, 3, 5, 7, 11, 13 among the first integer 30030 numbers, there are numbers which will not be obtained as the multiple of one of these prime numbers by the others.

There is another reason for proving the infinity of prime numbers which is old and it is easier in some features, but it can’t show clearly that how enormous is the number of prime numbers. This reasoning is as follow:

We prove there is at least a number which is greater than an arbitrary integer number "n". If we show the multiplication of first "n" integer numbers by "n!" and identify "N" by the following relation:

N=n!+1           (1)

Then if "N" is not a prime number, it must have at least one prime divisor "p". This divisor "p" can’t be smaller or equal to "n", because according to relation (1), if we divide "N" by a number like "a" which is between 2 and "n" then the residual of division will be equal to unit. It means that "N" isn’t divisible by "a", therefore, there is a number like "p" which is greater than "n". Since the number of prime numbers is infinite, the distance between two consecutive prime numbers can be arbitrary great. We will show how we can use the decomposition into the positive prime factors in calculating the number of divisors and the sum of them.

1.8. Functions and

1.8.1. Definition

If "n" is integer and positive, then we show the number of positive divisors of "n" by and the sum of all of the positive divisors by.

In the following theorem, we obtain a formula for calculation  and by using the decomposition into the prime factors.

1.8.2. Theorem

Suppose , therefore:

And also:

Proof: suppose  is a positive divisor of "n". For each "i" we have , then, for all "", there are  different selections.
(In fact . Therefore, we can select the powers of  in different ways. Then:

For calculating , at first, note the following product:

This multiplication is equal to the sum of all possible products of so that .

But family of all of these products is exactly equal to the sum of all of the positive divisors of "n" therefore . For completing the proof, at first we consider:

(For prowling, it is enough to multiply  by )

Therefore, we have:

1.8.3. Remark

The function  and are examples of number theory functions. They have common and very important qualities. Both of  and are multiplicative, it means for both of two coprime numbers "m" and "n", we have:

Generally, the function "f ", which is defined on set of positive integer number, is called multiplication if and only if for all "n" and "m" that:

For proving multiplicative of and, we can gain some results directly and with some calculations and with use of some formulas.

Function-Euler is another important multiplicative function that we acquaint it here.

1.8.4. Conclusion

 If "P" be a prime number:

 (: Euler's Function)

Proof. This assertion is clear for "k=1". Since if "P" be prime:

If , since "P" is prime, then the numbers which aren’t coprime with are as follow:

Therefore, the number of numbers aren’t coprime with "P^k" is equal to "P^k-1" and the other numbers are coprime with to "P^k". The number of them is equal to ""or  that here, assertion is proved.

1.8.5. Result

We know that if (a, b, c,…) =1, then:

Therefore, we can write for (p, q, r, … are prime factors):

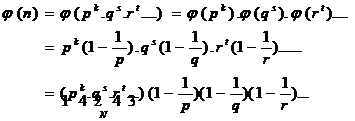
So:

For example, the number of numbers smaller than 100 that are coprime with it, is calculated with below method:

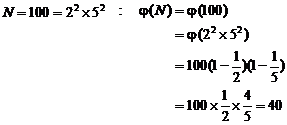
1.9. Perfect numbers

1.9.1. Definition

We call integer number n>0 as Perfect, if it equals to sum of divisors smaller than itself. Therefore, "n" is perfect if and only if  that  is sum of divisor of "n" (with itself). Mental principle of perfect numbers roots back to ancient Greece's times and we must search it in history. Greeks had a lot of secret properties for these numbers. Greeks mathematicians had very tendency to these numbers. Although they knew only 4 perfect numbers in Euclid themes that are: 6, 28, 496 and 8128.

In spite of this little and deficit information, they guessed even perfect numbers finish with 6 or 8 that 5th and 6th number of perfect numbers are 33550336 and 8589869056 that both of them finish to "6". Of course this result is correct that perfect number finish with 6 or 8. Euclid mentioned below method for calculating perfect numbers in book "preliminaries".

1.9.2. Theorem’s Euclid

Suppose  be prime, then  is a perfect number.

Proof. Suppose  that . Since "p" is prime, then divisors of  are in or  form clearly .

Therefore:

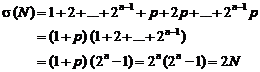
Therefore "N" is a perfect number.

Natural question that propounded is that we ask:

Is the inverse of this Euclid theorem established? Are all of perfect numbers, in mentioned form in (1.9.2)?

Almost, 2000 years after that, Euler answered it.

1.9.3. Remark

 Euclid algorithm isn’t an organized method for calculation of highest common divisor of two numbers. Euclid expressed and proved this algorithm in his book "Preliminaries". Of course, may be this algorithm was known before Euclid, below lemma is key of understanding Euclid algorithm.

1.9.4. Lemma

 Suppose "m" and "n" are integer numbers that both of them aren’t "o" together. So, for every correct number:

1.9.5. Theorem’s Euler

All of the even perfect numbers are in form which  is a prime number.

Proof. Suppose "N" is an even perfect number. At that rate .

Put , which  and "m" is a prime number.

Since and is a multiplicative function, we will have:

With solving the equivalence , with respect to  we will have:                                   

      (2)

Therefore, is a integer number. Then both "m" and   are divisors of "m". Because,, from this we know that "m" and  are only the positive divisors of "m". So, means   and in the result "m" is a prime number.

Here, we remember two problems about perfect numbers.

The first of them is this odd perfect number. So, we know if there is an odd perfect number, it must be greater than 10³⁰⁰ and therefore it has 8 distinctive prime factors at least.

With these descriptions, we can result that there isn’t odd perfect number.

The second problem is none response until now that, Are the number of perfect numbers infinite? In the primary ages they have known four perfect numbers which considered before.

But the fifth of these numbers hasn’t been discovering until 15th century, till now, we know 42 even perfect number (2005). The first, 21 of them have been discovered to 1900.

For example, the known perfect number 2⁸⁵⁹⁴³² (2⁸⁵⁹⁴³³-1) is an ogre of mathematics with 517430 Digit almost. Then existing infinite perfect numbers remain an open problem till now. Now after determination the highest prime number of 21 century, in fact the highest perfect number calculates also:

The highest known perfect = 2^25964950(2^25964951-1) number of year 2005.

We finish this section with mention some important theorem about prime numbers like Bertrand’s principle. We know that Bertrand principle propound existing of prime numbers between numbers "n" and "2n".

Joseph Bertrand propounded his guess in 1845 and searched it for numbers between "1" and "3,000,000". But Russian mathematician Chebyshev solved it logically. Although its proof is easier than prime numbers but "1" remember.

Remember only its stronger results.

1.10. Bertrand’s principle and theorems of

Chebyshev, Dirichlet and Poisson 

1.10.1. Bertrand’s principle

For every n>1, a prime number exists between "n" and "2n". Stronger result of Bertrand principle is:

1.10.2. Result

If "n>5", then at least two different prime numbers exist between "n" and "2n". Another obvious result is that inequality "" results

1.10.3. Generalization

In 1892 Bertrand’s principle extended by James Joseph Sylvester in below from:

If "m" and "n" be two positive integer numbers and m>n, then at least, one of numbers m+1, m+2, …, m+n   has a prime divisor greater than "n". (With thesis that m=n+1, Bertrand’s principle is resulted)

Another important theorem about prime numbers is Dirichlet’s theorem that if "a" and "b" (a0) be coprime, then infinite prime numbers exist in "ak+b" form that kn. It is obvious that if "a" and "b" have common factor greater than "1", then for every integer number "k", "ak+b" is a compound number.

For example, existing of infinite prime numbers in "4k +3" and "4k +1" form is obvious.

1.10.4. Dirichlet’s theorem

Suppose "", "" and . Therefore infinite integer number "k" exists. So that "ak+b" is "a" prime number.

Dirichlet’s theorem is the first important application of analytic methods in number theory. In fact, Dirichlet’s theorem and prime numbers theorem are two important theorems of primary theory of numbers that are solved by analytic methods. For both of these two theorems, primary proofs exist that it doesn’t use deep theorems of functions theory. But expressing of their proof is so hard that it isn’t in frame of this book.

Now, we propound a combination of prime numbers theorem and Dirichlet’s theorem:

1.10.5. Poisson’s theorem

Suppose "a" is a positive number and (a, b) =1 and it defines is the number of prime numbers in ak+b form and smaller than "x". Then we can approach quotient of  sufficiently to, if "x" is great sufficiently.

1.10.6. Remark

Limit of doesn’t depend on choosing "b" until "a" and "b" are coprime. Quotient tends to a limit that only depends on "a".

1.10.7. Result of theorem (1.10.5)

If "" and "" are sets of digits so that e_n are odd and "", then there will be infinite prime numbers so that start with digits "" and finish to "". Theorem (1.10.5) has very beautiful interpolation that probably it doesn’t see obviously from above propositions.

Fore example, if "", then it is resulted from theorem (1.10.5) that (since "") half of prime numbers are in "4k+1" form and another half is in "4k+3" form. (Exactly, we can approach the ratio of "" to ½ for "x" that is sufficiently great). Therefore, we can find out from theorem (1.10.5) that if "", then a quarter of all prime numbers are in "8k+5" form and the last quarter in "8k+7" form. Generally, with supposing "", if "" (mod a) then "n" is in form if and only if "n" is in "" form.

So, we can only calculate different values for "n" So that "a" and "b" are coprime. Therefore, it is resulted from theorem (1.10.5), that for every permissible value of "b", sequence of the numbers "a, a+b, a+2b ..." includes the equal ratio of prime numbers, it means that the ratio of prime numbers is .

1.11. Lagrange’s theorem

Suppose "p" is a prime number and "n" a natural number then the greatest power of prime number "p" in "n!" is equal to:

(: Number integer part).

Proof. We want to count the number of prime factors of "p" in "n!".

The number of integer numbers among the numbers "1, 2, …, n" that "p"

aliquot them, is equal to .But some of these numbers are also divisible by "". Specially in the sequence 1, 2,..., n, the number of numbers divisible by "" are exactly equal to and etc.

Therefore, sum of is equal to the number of prime factors of "p" that exists in n! ; It is necessary to mention that this summation has always a finite number of non-zero terms. Because for supposed "n", there is "k", so that, therefore, .

On the other word:

We suppose numbers "n" and  as natural number and  as a prime number. It is clear that numbers of  sequence are divisible by must be in  form that  is a natural number and adapted in condition  in which. It is obvious that the number of   values is. In the other hand "t" ("p" power) that appear in factorization of "n!" to prime factors n is obtained from sum of numbers which are the number of  sequence’s terms divisible by  or or or ... .Therefore justification of relation (1) is verified.

1.11.1. Example

Calculate the greatest power of that aliquot "62!".

Solution. According to and considering this point that greatest power of "5" is smaller than the greatest power of "3" which aliquot "62!", it is enough to determine the greatest power of "5" which aliquot "62!":

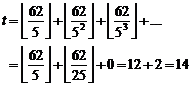
It is obvious that the greatest power of "3" which aliquot 62!, is the least "14". So, the greatest power of "15" which aliquot "62!" is "14" (number ).

1.11.2. Example

How many zero the number 100! is ended to?

Solution. In fact, we must calculate he greatest power of in "100!". Since the greatest power of "5" is smaller that the greatest power of "2" which aliquot 100!. We determine only the greatest power of "5" that aliquot 100!:

Therefore, 100! is ended to "24" zero.

1.11.3. Example

How many zero the number  is ended to?

Solution. The greatest power of "10" that aliquot "340!" is:

And also, the greatest power of "10" that aliquot "170!" is:

Therefore, number is ended to "83-41=42" zero.

1.11.4. Example

Find natural number "n" in which "n!" is ended to "20" number of zero.

Solution. It is clear that number "n!" is ended to "20" number of zero if and only if the greatest power of "5" that aliquot "n!" is equal to "". On the other hand we want to find "n" that

If "", then and if , then "", therefore, it is clear that.

If , then, we can write:

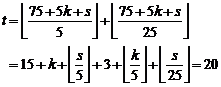
If and, then:

   ; 

Therefore, values of "n" will be determined for  and "":

;

1.11.5. Example

If we suppose that "n!" finish to  the number of zero, show that is approach to  for great number of "n".

Solution. It is clear that is equal to the greatest power of "5" which aliquot "n!" (According to theorem 1.11):

          (1)

It is obvious that if , then  and it means that there isn’t more than "" nonzero terms in . Here, we consider below geometric progression:

                        (2) 

With comparing every term of (1) series with every term of (2) series:

In special case:

       (3)

The limit of infinite terms of geometric progression (2) is equal to , so, we have below relation with substituting this value instead of:

(In fact, if "n" be great infinitely,  is great infinitely)

             (4)

Since the rate of changing of logarithmic function is slower than "n", then if we choose "n" great enough, we can approach the quotient of  to so that is equal to "n/4" approximately.

1.11.6. Example

Whether number "n!" can finish to 48 number of zero?

Solution. It is clear that for solving this problem, it is enough to determine the greatest power of "5" which aliquot "n!" . For, we calculate:

[1]. Fermat was a lawyer. He was expert in ancient languages and has high rank in classic culture. At that time, no scientific journal existed and he didn’t like to write his demonstrations. In stead of it, he had correlation with priest M. Mersenne who had coherence to all of European scientists extensively. Fermat took the lead in analytic geometry from Decartes and in differential calculus from Newton and Leibniz, but his work didn’t become famous, because he couldn’t print his book in these fields. His celebrity is because of his work in number theory, that he hasn’t any match in this field.

[2]_. Some bodies believe that Guass is greatest mathematician till now. He guessed theorem of prime numbers in 15 years old, he determined characteristic of construction able polygon in 18 years old. In 22 years old he proved that a polynomial of "n" the degree has "n" roots, and printed his best work as Disquisitiones Arithmeticae when he was 24 years old. This book changed numbers theory from set of singular problems to a branch related to mathematics. After 1801, he studied other field of mathematics, mostly geometry, analysis, astronomy and physics except two essays about two quadratic reciprocities. He spent his accomplished life in Guttingen University. His gathered works included 12 books.

[3]. Lambert’s family was poor and he had to leave the school at the age of 12, and after that he had no systematic adduction. Never the less, he has a considerable role in philosophy (acquaintance and metaphysics), astronomy (nebula), physics (optics, hygrometry and thermodynamics) and drawing.

His major work in mathematics (except of number theory) is in geometry and his book about parallelism and perspective was a background of nun-Euclidian geometry that came true in 19-th century.

He had a position comparable to Euler in Science Academy of Prussian only for the last 12 years of his life. Before that he was a teacher in his home land Swiss.

[4]. It can be written:  480 = (3-1) (5-1) (7-1) (11-1)

[5].Among the numbers which are in the form (4), we must omit the multiples of "11" among each of 48 numbers which aren’t divisible by 2,3,5,7.