CHAPTER 10
On the history of determining "k-th"
prime number by bounds for "
"
(determining lower and upper bounds for"")
10.1. Determining the bounds for "Pk "
(the" k-th "term of the sequence of prime numbers)
One of the important problems related to the prime numbers, is their distribution among the natural numbers that has a lot of unsolved problems. This theorem reveals the dispersion of prime numbers and shows that they are dispersed in natural numbers set like some individual oasis in a very expand desert.
10.1.1. Theorem
In natural numbers sequence, there are some intervals, with no prime numbers, that are as expanded as can be imagined.
First proof. If "n" is an arbitrary natural number, between "n" successive natural numbers:
The first one is divisible by 2, the second one by 3 and ….
The nth number is divisible by "
".
Second proof. Suppose that "p" is a prime number, as big as we want and "a" is the multiplication of all prime numbers from "2" to "p".
It is clear that all these successive natural numbers will be composite:
10.1.2. Remark
In contrast with these theorems, this theorem is established
that if "
", then there will be at
least one prime number between "n" and "
".
This theorem was stated by Bertrand in 1845 and was proved by Chebyshev in 1850
for the first time.
Another theorem has been proved in higher level that Serpinski published it in his book (pp. 284-296).
10.1.3. Theorem
If "
" (natural number), there
are at least two different prime numbers between "n" and
"
".
10.1.4. Result
If "
" is a natural number
between, there is at least one prime number "n" and "".
Proof: According to Chebyshev's theorem, this assertion is true for natural number greater than "3". It’s also true for "2" and "3", because there is "3" (as a prime number) between "2" and "4" and there is "5" (as a prime number) between "3" and "6".
10.1.5. Result
For "
" (natural number), if
"
" is as symbol for kth
prime number, it’s possible to write "
" and
"
". It for the natural number
"k", the inequality "
" is true.
According to result (10.1.4), there is at least one prime number between the
numbers 
and 
that is more
then "
".
Therefore inequality 
is true as a
mathematical induction.
10.2. Bounds for Pk from below and above
I. Lower limit of:
(1)
(2)
(3)
II. Upper limit of:
(4)
(The first inequality is strict for k>1)
:
(5)
One of the inequalities that are extractable by primary methods is show in the theorem below. The demonstration of this theorem shows that in number theory, it is possible to extract interesting results from a few preliminary acknowledgements.
10.3. Bonse's theorem (1907)
In prime number sequence, always:
10.3.1. Note
Bonze’s inequality, as we have mentioned about other
preliminary inequalities concerned to prime numbers, is too weak. For example
its information about "
" is:
, although
10.3.2. Remark
If "
", then:
10.4. Theorems concerning consecutive prime numbers
10.4.1. Theorem
If "", then:
Proof. Suppose that ""
then
.
According to theorem the proved is at least two prime
numbers between 
and 
. Therefore,
since the prime number immediately after is 
and
after 
is 
then
necessarily 
therefore, always
.
10.4.2. Theorem (Ishikawa, 1934)
If "
", then:
10.4.3. Remark
Prove that if "" then in
canonical factorization of "n!" there is at least one prime
factor with exponent "1". Consequently, if "m" is an
arbitrary natural number except of "1", for "",
"n!" will never be a perfect m-th power.
10.4.4. Theorem
If "n" is a natural number greater than "5", there will be at least two prime numbers greater than "n" and smaller than "2n".
10.5. Theorems of Chebyshev (1850)
10.5.1. Theorem
If "
", then there is at least
one prime number like "p" so that 
.
Proof (Ardoosh, 1932). For "n=4" and
"n=5" validity of assertion is obvious by testing. So, we
suppose that "
". According to the
previous theorem, there is at least, two prime numbers like "p"
and "q" (
) so that
.
Now if "
" then, because ""
is a composite number and "
", then "
".
But if
, then: 
.
10.5.2.Theorem
If
, then:
10.5.3. Remark
If we choose one of 
or 
instead
of
, the relative error can be
restricted as follow:
,
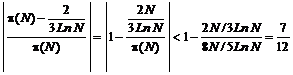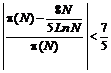
So, for every positive number "
"
after an order:
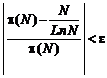
10.6. Theorems of Ishikawa (1934)
10.6.1. Theorem
If
,
and
, then (
):
10.6.2. Remark
Hardy and Littlewood have guessed (1923) that for every two natural numbers "m" and "n" which are non-one:
But this assertion neither has been proved nor disproved.
10.6.3. Remark
If "
" is the n-th prime number,
since
, then:
10.6.4. Theorem
For every two natural numbers "n" and "m":
Proof. For "
" the
assertion is clear and for "
" the assertion is proved by
using below inequality and according to theorem (10.6.1), 
and 
:
; 
Here it is proved with using presented theorems and lemmas:
10.6.5. If 
then:
10.6.6. If 
then:
10.6.7. If 
then:
10.6.8. If 
then:
