CHAPTER 13
Decisive solution to Riemann zeta equation 
by
the determining function concerning the precise
number of primes 
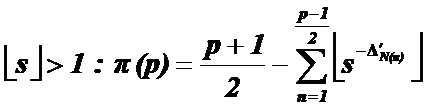
13.1. Riemann’s zeta function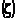 
We know that Riemann’s researches are based on 
famous
function:
(1)
According to
,
series of second side is a concurrent series. And we can write:
(2)
In second side, all of prime numbers appear, because in relation (1) all of natural numbers exist. In general case:
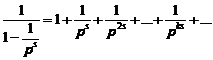(3)
If we multiply all of inequalities of (3) to each other:
(4)
It is obvious that
"
"appears only one time and
chooses all of possible powers from zero to infinite. Relation (4) is
equivalent with relation (1), because every integer number can be decomposable
to multiplication of prime numbers in only one form.
We know that rule of "rarefaction"
of prime numbers is based on that the number of prime numbers less than "x"
asymptotically is equal to "
":
(5)
According to recent relation, rule of "rarefaction" of prime number can be written in form of an equation[1]:
(6)
In fact equation (6) is solvable when find an exact relation that with help of it the number of prime numbers, can be found.
It is obvious that function "
"
which its approximate relation is defined by (5) is an approximately solution
for equation (6), because asymptotically they approach to each other. In fact,
with presenting an exact relation for
, we solve
Riemann’s zeta function (6).
13.2. Decisive solution to Riemann’s zeta equation (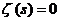
)
(Millennium Prize Problem)
In section (4), decisive solution about problem of the
numbers of prime numbers definition, presented by identification function 
exactly:
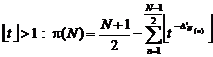(7)
It is clear that according to relation (2), it is enough to put "N" and "t" instead of "p" and "s" in relation (7)
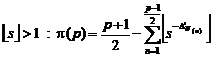(8)
In fact relation (8) is a solution for Riemann’s zeta
equation (6). Because for every "p" with condition , 
is
equal with the number of prime numbers not more than "p", can
be determined exactly. Now, we show application of relation (8) by an example.
In general case, below table can be formed:
|
|
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
… |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
… |
13.2.1. Example
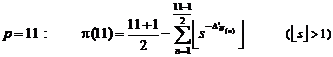
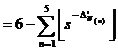
[1] .We know that this problem is one of "7" international unsolved problems. The clay mathematics institute (CMI) of Cambridge, Massachusetts has named seven "millennium Prize Problems". The board of directors of "CMI" designed a $7 million prize found for the solution to these problems, with $1 million allocated to each. The "CMI" web site at: http://claymath.org/Millennium_Prize_Problems/Rules_etc/