CHAPTER 14

On the history of searching for famous prime numbers and the factorizations of these numbers

14.1. Some of famous numbers

Some of the forms of numbers exist that verifying in them, was origin of important improvements in number theory. Some of them that had old record like figurate numbers, perfect numbers and amicable numbers that found favor not only because of their interesting Arithmetical properties, but also because of secret properties that had attributed to them, and others are Fermat's numbers, Mersenne's numbers, Fibonacci's numbers and lucka's numbers.

14.1.1 Theorem

 If "a" and "n" be two non-one natural numbers, in order to  be prime necessary conditions is that  and "n" be prime, but this conditions aren’t sufficient.

Proof. With suppositions, we suppose that () be prime number. If, then and and this is paradox with being prime of (), so. For proving the assertion about "n", if "n" is not prime, natural numbers like "h" and "k" exists so that , and .

Then in one side and the other side and therefore and also it is paradox to primality of. Proving the insufficiency of condition is by counter example, it means () has mentioned but it is equal to:

14.1.2 Theorem

If  and, in order to () be prime, necessary condition is that "a" be even and "n" be a power of "2", but these conditions aren’t sufficient.

14.1.3. Theorem

If "p" be an odd prime number, every positive divisor of "" is in "" form, that "k" is a non–negative integer number.

Proof. It is clear that divisors of ""are odd. So assertion is established bout odd prime divisor of "". For finishing demonstration, it is enough to observe Firstly, "1" is in ""form  and secondly multiplication of every two numbers which are in this form, is the same.

14.1.4. Theorem

 If , then every odd prime factor of is in form that "k" is a natural number.

14.1.5. Theorem

(Fermat in his letter to Fernikle in 1640), If "p" be a prime number and greater than "3", every non–one positive divisor of "" is in "" form that "k" is a natural number.

Proof. First because "", so "N" is a natural number.

Now, we consider that d|N and. For proving the assertion, it is enough to prove that every prime factor of "d" is in form. We consider that "q" be a prime number and q|d. Because "N" is odd and. At first, we prove that. We consider that, So, 3|N and and then. Therefore, because order of "2" is "6" with module "9", so 6|2p and then 3|p is opposite of thesis.

So, it is clear that. Since q|N, in the above mentioned way, it will be clear that. Now we consider that "h" be order of "2" with module "q". Because none of and are divisible by "q" (Because ),  also  and . So even numbers "2p" and () have common divisor greater than "2" and so. So, because "p" is a prime number and , then . At last, because () is even and "p" is odd so and then .

14.2. Fermat’s numbers

For every, we name the integer number as Fermat’s number. If ""be prime number, then we call ""Fermat’s prime number or Fermat's prime.

If "n" be equal to one of " and 4", then "" are respectively "3, 5, 17, 257 and 65537 "that all of them are prime numbers. Maybe important, reason of renown and importance of these numbers is that in "1640", Fermat claimed in a letter to Fernikle that "" are prime numbers for every . And as usual, Fermat didn’t present a demonstration for it. But in "1658", he claimed that with infinite decreasing method, he proved it. In fact, this guess was false. Almost a century later, in "1732", Euler showed that "641" is a divisor for "". In "1640", Fermat gave an answer to Fernickle in a letter and showed that "" isn’t a prime number and "223" is a divisor of it. In fact, Fermat showed that divisors of  " " are in "" form. In fact, we can present use the same Proof for  that if "p" be a prime divisor of "", then "p" must aliquot . We can prove that  that "k" is an integer number. First prime numbers of this form are 193, 257, 577, 641, … that 641 aliquot "". In fact, this is such method that Euler showed that "" isn’t prime and it is so strange that why Fermat couldn’t prove it himself and he didn’t use the method which was used for calculating the factors of "", for factorization "". With more attention, we can show that prime divisor of "" are in "128k+1" form, not in "" from.

We avoid proving of this subject in this book. In next subjects, we show that same results are established for prime divisors of Fermat's numbers "".

14.2.1. Attention

Fermat’s numbers are very important not only for their interesting arithmetic properties, but also for their perfect dependence to dividing periphery of circle to equal members by compass and star.

14.2.2. Theorem

(T. Pepin. 1877). If and only if "" be prime numberthen:

Now, we explain these problems below:

How is it possible that we know compositing of a Fermat’s number without knowing a divisor of it?

Answer of this question will clear in explanation of using of Pepin theorem. If be congruent with "-1" by module "", then "" is prime. If not, it is composite.

Now, at first we choose simple example of "". We must search that ""is in ""form or not, because. Method of calculation is clear for reader. With module,   ,, ,

,,

So"" is a prime number. As it seems, we just need to calculate of square of a number and changing to module "" in above calculation. And this reduces, save us that we entangled with such a big number like"".

Generally,  and we must calculate square of "3" of () times and after every times, reduce out come to module "". If final result be congruent with "-1" by module "" then "" is prime, if not, it is composite (attend that if "" be composite it hasn’t any factor of it).

And for "" we must repetition it action () times and after every times, changing to module (This number has 39 digits). Therefore we must calculate square of a number with at least 39 digits, 127 times and we divide out come of every times by, a 39-digit number and calculate residual of division.

These calculations are very tedious, but possible and with this method, in 1905 Morehead and Western could prove compositing of "" without they could present a divisor of it. Of course with new electronic computers, we can determine primality of greater numbers according to this principle.

14.2.3. How did a divisor of 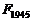 be obtained?

According to previous theorem every prime factor of "" is in form of ""; this assertion was in one of Euler’s works (in 1747) and maybe he knew it in 1732 (when he prove compositing of ""). In 1877, Luka proved stronger theorem.

14.2.4. Luka’s theorem

Every non–one divisor of  is in form. According to Luka’s theorem, divisors of are in form. For , Tivial divisor "1" will be gained. Now, we search about prime divisors of . Out come numbers aren’t prime for and , because  and , and this number is divisible by .

Out come number is also composite for, because:

So, Also, out come number is composite for. Now we test that has 587 digits. We observe:

Is  divisible by "m" or not? Searching about it refers to searching about this that is divisible by "m" or not? For finding "", we must calculate square of 1944 number that every number has 587 digits at least, and after every action of square, we divide the out come number (that has 1175 digits at least) by "m" and calculate residual of division. Only new electronic computers can calculate these and so, Robinson could prove that . Therefore  is a composite number, because . Meantime, according to what we said at first about factors of  and about compositing of values of for 1,2,3 and 4 values from "k" it clear that "m" is the less non–one positive divisor of . So it is a prime number.

14.2.5. Lemma

If "p" be a prime number in form, then:

Proof. With testing, it clears that assertion is established for . So, we consider that  and . We show multiplication of natural numbers which are devisable by 3, firstly from 3 to P. It is clear:

.                  (1)

Now, we factorize "P" to:

.

It is clear:

So, , and according to (1):

But""and "p" is coprime with. So:

This is equal with congruence of assertion. (Specially the case of this lemma is Pepin’s theorem:).

14.2.6. Theorem

 If "",  relation  always is established.          

Proof. For every integer number, it is clear that  (Bernoulli’s inequality). Therefore ; so and so  that it results immediately.

14.2.7. Note

It is clear that Fermat’s numbers are pseudo–prime.

14.2.8. Attention

We can show that if for natural number "k", adapts in condition, then "m" is a Fermat’s number.  

Here, we express some special problems which lead to some special results about "" (Fermat’s numbers). Mentioned interesting special numbers are in  and form.

14.3. Special problems and Fermat’s numbers

14.3.1.

Find all prime numbers in form so that "n" is a natural number which hasn’t more than 300000 digits!

Solution. Only three prime numbers exist which adapt in conditions of problem:

, ,

In fact, if be prime, it is obvious that "n" hasn’t odd divisor grater than "1". So, it must be in  form, that "k" is an integer number. But in this situation "". We are sure that "k" hasn’t odd divisor greater that "1". Therefore,  that  is an integer number. Than that for ,  and for ,  and for  and  ,  and  are obtained respectively, that both of them are composite. For ,  is obtained that and latest number has more than 300000 digits.

14.3.2.

Find all prime numbers in form that hasn’t more than digits.

Solution. Only two numbers exist that are:

  ,  

We use the same proof as we used in previous problem. At first, we prove that if  and "" be prime, then that "s" is a natural number.

Therefore:

For are obtained that both of them are composite ( and) for ,  is obtained that has more than digits.

Now, we understand that if for every , be composite, then infinite Fermat’s numbers exist that are composite.

14.3.3.

In a letter to Fernickle, Fermat’s guessed that if "a" be even then is prime, except some "N" that are divisible by Fermat’s numbers. We reject this Fermat's guess.

Solution. We put  and , then . But 89 and 233 are prime number but none of them are Fermat’s numbers.

14.3.4.

If "" is an indicator of n-th Fermat’s number, prove that infinite "n" exist so that  is a composite number.

Solution. We remember that is square of "". Therefore, if "n" change from "0" to, then their values with module "7" are "2, 4, 2, 4, …". So if "n" be odd, then .

Therefore, for every (odd),  is a composite number.

14.3.5.

If , prove that "" finish to 7.

Solution. We prove that if , then  (mod 5). And "" is odd, so "" finish to 7. If , then , we put .

Therefore .

14.3.6.

Problem (14.3.4) is equal to that we prove infinite composite numbers exist between numbers in form and  .

Solution. We want to prove that all numbers in  form and  are prime numbers .In fact, we know that for every natural number "k",  that "t" is a natural number. So:

But, since for every natural number "k", so it is a composite number. Problem of existence of infinite prime numbers in form of "" is also an open problem.

14.3.7.

For every natural number "n", prove that  is a composite number.

Solution. All of this kind numbers are divisible by 3, so result is obtained.

14.3.8.

Numbers in form of and  can be decomposed by identity. Compositing of these two numbers can be proved by factorization.

(Guidance:)

14.3.9.

If "" be n-th Fermat’s number, It is proved simply that  isn’t a prime number for .

14.3.10.

We can show that infinite composite numbers exist between numbers in  form. (Guidance: it is enough to calculate with module 11).

14.3.11.

It is prove simply that if  then the Fermat’s number  is in  or form. Now, we express some properties of Fermat’s numbers.

(I)   .

(II).

(III).

Lemma. For every natural number "n":

In other word, every Fermat’s number except "", is in  form.

Proof. Assertion is established for. We Consider n>1 and . So, then according to (I):

14.3.12. Theorem

Every two different Fermat’s numbers are coprime.

Proof. We consider "" and "" are two different Fermat’s numbers and "d" is a positive common divisor of them. Without any disorder to generality, we consider that . So,  and because of (III), . But, according to definition of "d", .

So and  or  . But because "" is odd, , so .

14.4. Another proof for Euclid’s theorem

We suppose that there are only "r" prime numbers. We call them . Because every one of  numbers of  has a prime factor, according to pigeonhole principle, it is necessary that one of "" aliquot at least two numbers of these  numbers and this is paradoxical with theorem (14.3.12).

14.5. Speed of the growth of Fermat’s numbers

As it is clear from definition of Fermat’s numbers and also equality (I), Fermat’s numbers increase fast. For example,  has more than  digits.

How can we gain this result without logarithm tables? Simply, because:    ;

14.6. Fermat’s numbers and the problem of inscribing
 regular polygons inside a circle 

14.6.1. Gauss's theorem

Necessary and sufficient condition for dividing circle to equal "p" part by compass and star is that "p" be a Fermat’s primer number.

It is necessary to say that solving the problem of scribing regular "m" goons in circle lead to drawing the angle. In other word, if "k" and "t" be two natural coprime numbers, two correct numbers "u" and "v" exist that , so:

14.6.2. Result

For every two coprime non-one natural numbers, "k" and "t" if divide the circle to "k" equal members and "t" equal member be possible by compass and star, its dividing to "kt" equal members is also possible. For example, dividing the circle to "15" equal member is possible and manner of division is obvious with below relation:

Here, according to Gauss’s theorem and also division an arc to "" equal members is possible by compass and star, it is clear that if natural number "m" be a multiplication of  in one or some different Fermat’s prime numbers, dividing the circle to "m" equal member is possible by compass and star.

Until Gauss’s time, dividing the circle was known only to and equal parts. Because "" is a prime number, according to Gauss’s theorem, dividing the circle to "17" equal parts is possible by compass and star.

14.7. Refutation of Fermat’s assertion and factorization
of Fermat’s numbers

As we said, Euler was first person who proved falseness of Fermat’s guess by factorization "" to multiplication of two prime factors (1732). In 1880 Fortune Landry in 82 years old, proved after some month attempts:

(Both factors of second side are prime number). In 1905, C. Morehead and A.E. Western independently, proved that "" is composite without factorization it. Until 1971, none of "" factors was known, but in 1971, John Brillhart and Michael Morrison with help of an electronic computer in California University (Los Angles) decomposed this number to multiplication of  two prime factors and this is one of charming factorization that has been done till now:

In 1909, Morehead and Western proved untidily that "" is also composite. Today we know that "" is composite for below values of "n":

14.8. Mersenne’s numbers

Mersenne’s numbers are important because of two reasons at least firstly because of their perfect dependence to perfect numbers and secondly because greatest known prime number is one of these numbers. In this discussion, we acquaint Mersenne’s numbers and also a short history of searching about these numbers will be expressed.

14.8.1. Generalities in Mersenne’s numbers

According to theorem, if "":

              (1)

be prime number, it is necessary that "n" be a prime number. The ancient Greeks had known that  and  are prime number. In 1644, Mersenne said this assertion that "":

                  (2)

For below prime numbers is prime:

p = 2,3,5,7,13,17,19,31,67,127,257

And for other prime numbers of "p" that are smaller than "257", "" is composite. On the occasion of it:

14.8.2. Mersenne’s assertion is false

 and  are Composite and,  and  are prime.

Now, we know that "" is prime number for below 42 prime numbers (2005):

P =2,3,5,7,13,17,19,31,61,89,107,127,521,607,1279,2203,2281,3217,

4253, 4423, 9689, 9941, 11213, 19937, …, 25964951

And for the other prime numbers which are smaller than "", they are Composite.

14.8.3. Attention

Still it isn’t clear that sequence of Mersenne’s prime numbers is finite or not.

14.9. Problems concerning Mersenne’s numbers

A bout Mersenne’s numbers, below questions were proved:

1. If "p" and  be prime, only one of below relations is established:

   or  

2. With previous question, it is proved that  and  are composite.

3. If "n" be odd and pseudo–prime "" is also pseudo–prime.

4. If "p" and "q" be two different prime numbers.

5. "" isn’t m-th  power of any natural number.

6. Every odd number aliquot a lot of terms of sequence.

14.10. Perfect, imperfect and redundant numbers

14.10.1. Definition

Natural number

Is called as an perfect number when;

Is called as a imperfect number when ;

Is called as a redundant number when .

14.10.2. Remark

We consider that "a" be a natural number. We call a natural number "d" as a member of "a" "except itself" when  and . For example, members of "6" which are "except itself", are 1, 2 and 3. According to above definition, natural number "a" is perfect, imperfect or redundant with respect to that is equal with Sum of "except itself" "a" member or be greater or smaller than this sum.

14.10.3. Example

Numbers "6" and "28" are perfect:

6=1+2+3, (6) =1+2+3+6=2.6; 28=1+2+4+7+14

Number "9" is non-perfect and 12 is redundant:

9>1+3,  (9) =1+3+9<2.9;

12<1+2+3+4+6,  (12) =28>2.12.

14.10.4. Remark

If "p" be prime number and "" be a natural, "" is an imperfect number, because:

.

14.10.5. Remark

If "p" and "q" be two different odd prime numbers and "" and "" be two natural numbers,  is imperfect. So, set of odd imperfect numbers (even) is infinite.

Without any disorder to generality, we suppose that. Like previous example, it is clear:

According to suppositions,  and . So according to decreasing of :

14.10.6. Remark

Between "1" to "100", only "22" redundant numbers exist and they are even:

12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70,
 72, 78, 80, 84, 88, 90, 96, 100

Between odd natural numbers smaller than 1000 only 945 redundant numbers exist. Immediate redundant number after it is 1575.

14.10.6. Even perfect numbers

In theorem 36th, 9-th article of "Principles" book, Euclid proved that if "" be prime, even number of is perfect.

2000 years after it, Euler proved that Euclid’s formula perfect obtained all of even perfect numbers.

14.10.7. Theorem

If  be prime number:

                (1)

Is perfect (Euclid). Contrarily, If "a" be perfect and even number, there will be a natural number like "n" so that  is prime and equality (1) is established (Euler 1749). So, even perfect numbers are"." for every "p" prime number that "" be a prime Mersenne’s number.

Proof of Euclid assertion. Suppose that be prime number and  since, then according to being multiplicative of "" function:

14.10.8. First proof of Euler’s assertion (Euler)

 Suppose that "a" be a perfect and even number. So  that  and,. According to thesis, . So since:

(1)    ,

and also:

(2)    

So, because latest fraction is unchangeable and standard, for every natural number like "c":

(3)            ,      (4)     

Then, . Because, if we consider that c >1, so "b" has divisors of "b", "", "c" and "1", therefore:

So:

and it is opposite of (3). So  and according to (3) and (4),  and , then, "b" is prime. So, if , then   is prime and .

14.10.9. Second proof of Euler’s assertion

This proof belongs to Dikson (1929) and it is branch of Euler’s proof. With considerations and symbols of Euler’s proof, according to (1) .  So, for natural number like, "c", (i) "" and (ii) . So, (iii) . But, according to (ii), " and ". Therefore, "b" has two divisor "b" and "c" and because of (iii), it hasn’t another divisor. Then . So "b" is prime and according to (ii) . Therefore .          

14.10.10. Remark

As it is clear from previous theorem, Problem of even perfect numbers definition has completely dependence to problem of prime Mersenne’s numbers definition, and since it isn't clear that sequence of even perfect numbers is finite or infinite.

14.10.11. Theorem. Every even perfect number is ended to "6" or "28" .In other word, for every even perfect number like "a" one of below congruencies is established:

  ,  

Proof. Suppose that "p" is an add prime and  is a perfect number. If "p" be in or  form, there is two case.

First case. . Because natural powers of "16" finish to "":

, and .

Second case. . So . Moreover, as it seemed past, it is clear that . The gist of the matter  ended to "4" and it is divisible by "4", so, according to rule of divisibility by "4", is finished to 04, 24, 44, 64 or 84. In every one of these cases, that "t" is a correct number. Then,  and also:

14.11. Historical remarks concerning (even) perfect
numbers and Mersenne’s numbers

Every where, mentioned "perfect number", its purpose is even perfect number.

14.11.1.

Perfect numbers are mentioned in Plato’s works. Old Greeks had known that these numbers like regular polyhedron, maintained completely harmony as it was in the world, and considered these numbers as reflection of this harmony. And because of their effect, in ancient times and early Middle Ages, every where, had maintained for these numbers, hinted meaning.

14.11.2.

We mentioned dependence of definition of even perfect numbers to definition of prime Mersenne’s numbers, before. Generally, problem of primality identification of  in general case is unsolvable and for big values of "p" has great difficulties. So, old mathematicians had false assertion about even perfect numbers. Old Greeks had known below numbers as prime numbers:

, , ,

And Nicomachos (the 1-th. century A.D), had known the like perfect numbers:

2.3 (=6), 2².7 (=28), 2⁴.31(=496), 2⁶.127(=8128)

And they supposed these numbers finished to "6" and "8" successively. Both of two suppositions are false. 5-th perfect number is 33550336 that first clue is in a European manuscript in 1456. In other side, Successive even perfect numbers like p=19 and p=31 are:

2¹⁸(2¹⁹-1) = 137438691328

               2³⁰(2³¹-1) = 230584 3008139952128

that both of them are finished to 8.

14.11.3.

We return to primality problem of. Maybe the first person, who attended that it isn’t necessary for to be prime number for every prime number of "p", was Hudalrichus Regius, who presented factorization of  in 1536.

14.11.4.

In 1644, Mersenne’s assertion published and became origin of extensive researches. Euler (1772) verified that  is prime number. So, he calculated   8-th prime number. Describing all of researches that has been done about primality of Mersenne’s number doesn’t Contained in this brief. We mentioned some of the important works.

14.12. Role of computers in searching large prime numbers

Before electronic calculators, domain of research in number’s primality was very limited. Invention of normal calculators, facilitated calculations to some extent, But it was very weak in contrast of number’s greatness. In this time, wonderful speed and power of electronic computers had used and these computers, with help of some special criterion that scientists of number theory discovered them, could do excellent works and we mention some of them in next pages . Fore example, today we know that number  is a prime number, but it is estimated that If "80" persons calculate it primality with normal method; they must spend one thousand years. It mustn’t forget that power of electronic computers also is limited and for example, neither science and nor modern technology could clarity situation of (from Fermat’s numbers) about its primality.

Attend to this point that in past it was possible that a number could keep its topic as "greatest known prime number" as below number with "39" digits:

2¹²⁷-1=170141183460469231731687303715884105727

That in 1877 Lucka proved its primality. And because of it, this number is famous as Lucka's prime number. It was the greatest known prime number till 1951. In 1876, Lucka propounded that his long calculations proved "" is composite[1]. In 1903, Cole decomposed this number to multiplication of two prime factors:

M₆₇=2⁶⁷-1=193707721.761838257287

In 1883–87, "Pervusin", priest of "Perm" government (in Russia) and "Paul Seelhoff" from Germany, independently proved that inspire of Mersenne's assertion, "" is prime. In 1911, "Powers" proved that "" is prime number with use of a criterion which Lucka established. In 1914, Fauquembergue proved that "" is prime number. In 1922 Kraitchik proved compositing of below number:

M₂₅₇ = 231584178474632390847141970017375815706539969331281128078915168015826259279871

And Lemmer test validity of his work (1931). Lemmer with help of a table–calculator spent more than 700 hours on this work. After 20 years (SWAC) an electronic computer in California university (American) did this calculation in "48" seconds. (Generally, every minutes of SWAC’s work is equal with one year work of human with table calculator).

This was a short history of discovering Mersenne's assertion errors. For positive aspect, we just mention this subject that in 1877 Lucka proved by his self formula that the "39" digits number of "" is prime. This number was the greatest known prime number till 1951. For finishing the subject, we must say that in this year, "Ferrier" a French, calculated with a different method of Lucka’s method and by calculator that the "44" digits number is prime. This is the greatest prime number (and probably it will be) that is calculated without using electronic calculators.

In 1947, situation of all of Mersenne’s numbers from primality aspect for  was determined with or without using calculators.

Searching in "" for, isn’t possible and because of it Lucka’s prime number (M₁₂₇) till 1951 kept its title as "greatest known prime number".

14.12.1.

After 1952, the situation changed. In that year, with use of "SWAC", electronic computer, it was clarified that below numbers are prime number:

(Respectively have 157, 183, 376, 664 and 687 digits). The first known prime number has more than 1000 digits  that in 1961 by a kind of "IBM7090" calculator could prove its primality. In 1963, it is clears that  is prime number. (ILLIAC II) calculator of American university calculated this and it took long "2" hours and "15" minutes.  has 3375 digits and for sometimes, it was greatest known prime number. Till in 4-th night of March in 1971, Tuckerman proved that  is prime number and calculated it by a kind of "IBM" calculator[2].

14.13. Odd perfect numbers

What we said in previous pages was about even perfect numbers. One of famous and unsolved problem of number theory is that odd perfect number exists or not?

If such a number exist, at least have three odd prime factors.

Proof of odd perfect numbers related to solving below equation:

That every thing is indeterminate except this point that "" is odd prime numbers. Verifying in this equation is very complicated and till now, except some special condition of its possibility, we don’t know about existing answer.

14.14. Special problems concerning perfect numbers

14.14.1.

Prove that every perfect number is ended to "6" or "8".

Solution. Every even perfect number "N" is in  form that "p" is prime number. If , then . Therefore, consider that "p" is an odd number. If, then.

Also .. So, .If , thenand.

Therefore .

14.14.2.

Consider that  be a perfect and even number. Prove that "N" is in "" form.

Solution. Every even perfect number "N" is in form that "p" is a prime number. Specially if , then "p" is an odd number. For odd numbers "n", we show that (mod 9). If "n" be an odd number 1, 3, 5,… then is congruent with 1,4,7,1,4,7,… with module "9". Although, for odd "n", is congruent with 1,7,4,1,7,4,... with module "9". By multiplying these numbers is congruent with 1, 1, 1, 1, 1, 1, …with module "9". So:

14.14.3.

Prove that if "p" be prime number, then "" isn’t perfect number.

Solution. First method. According to definition of perfect number, sum of divisors of "" must be equal with , although, sum of divisors of  is equal with . Of course, it isn’t equal with 2p^k and infact; it isn’t equal with any other coefficient of "p". So, it is obvious that "p" doesn’t aliquot .

Second method. Because:

   So,  .

Therefore "" can’t be a perfect number.

14.14.4.

Prove that "n" is a perfect number, if and only if .

Solution. If "d" change on positive divisors of "n", then also take all of different divisors of "n".

Therefore, so "n" is perfect, if and only if  that with dividing two side by "n" proved our problem.

14.14.5.

With help of previous problem or every another method show that none of proper divisor of a perfect number, isn't a perfect number.

Solution. Consider that "n" be perfect and "k" be a proper divisor of "n". According to previous problem, now, attend that every divisor of "k", is divisor of "n". But "n", at least has another divisor greater than "k", for example "n". Therefore, . So "k" isn’t perfect.

14.14.6.

If "p" and "q" be two odd different prime numbers, prove that "pq" isn’t perfect.

Solution. According to multiplicative property of "":

.

That it isn’t equal with . Since for example  is divisible by "4", but  hasn’t such property.

14.14.6.1. Note. With same reasoning, we can show that multiplication of every the number of different prime numbers, isn’t perfect. Therefore, if an odd perfect number exists, it can’t be without square.

14.14.7.

Show that  is a perfect number.

Solution. It is enough to show that  is a prime number. In order to this, it is enough, we verify its prime divisor smaller than . Also prime factors of "" must be in form of"".

Therefore, it is enough that we test these prime numbers 103, 137, 239 and 307 that they don’t aliquot "". Since none of these number doesn’t aliquot "", so, "" is a prime number.

14.15. Problems on distinguishing Mersenne’s prime
numbers and Fermat’s numbers

14.15.1.

Show that is a prime number?

Solution. It is clear that every prime divisor of  is in  form. So, we verify only prime numbers smaller than and are in upper form. Because such a number doesn’t exist, so 127 is a prime number.

14.15.2.

Show that is  a prime number?

Solution. With help of problem (14.15.1), we verify only all of prime divisors of "q" that are in  form so that .

But the only prime number that in such kind is  and  then  is composite.

14.15.3.

Show that  is a prime number?

Solution. The only possible divisors must be in  form that are 59, 117, 175, 233, … it seem simply that 59 isn’t a divisor of it. And "117" and "175" also aren't prime number and it isn’t necessary to verify them. Because the smallest divisor of  must be prime and greater than "1". It seems simply that 233 is prime and a prime divisor of . So  isn’t a prime number.

14.15.4.

Show that "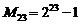" is prime?

Solution. Every prime divisors of  must be in  form 47, 139, 277,… . It seems simply that. So is composite.

14.15.5.

Consider "m" be an odd correct number. Prove that if "" then "m" aliquot Mersenne number. (Hint: use from Euler's theorem).

Solution. According to Euler's theorem, so that "k" is a positive correct number. Therefore "m", aliquots "", if "n" be a positive coefficient of.

14.15.6.

Prove that is a prime number.

Solution. We know that every prime divisor of "" is in form. We must verify all of prime numbers smaller than and in above form. We only find "193". It seems simply that "193" isn't a divisor of "". So "" is a prime number.

14.15.7.

Prove that.

Solution. It is proved with induction and we use Just properties of highest common divisor of two numbers. Consider "d" be constant. We show, if for every "s" and "t", assertion be established that  and , then assertion is established for every "s" and "t" that  and  also is established. If , then assertion is obvious. So, consider . According to relation :

Since "s" and "", both of them are smaller than "n" and also, so according to thesis of induction. So, always is established.

14.15.7.1. Note

With the same method, we can show that if , then:

14.15.8.

A. Suppose that "" be k-th Fermat’s number. Prove that if , then . (Guidance:  Suppose , then ).

B. With help of "A" propound another proof for infiniteness of the number of prime numbers.

Solution.

A. we can suppose . Consider "p" be a prime divisor of "", so , since is an extension to even powers of , so (mod p). Specially since "p" is odd, so "p" can’t aliquot "".

B. Every "", has a prime divisor like(Probably "" itself). Since, if , then , so  .If, then infinite different values of "k", obtain infinite different values of "". So, infinite Prime numbers exist.

14.15.8.1. Note

 We don’t need to know infinite "" are prime. In fact, this result is still an open problem.

14.15.9.

Suppose that  and and. Show that if , then "" and "" are coprime. (Hint. you can consider that , now show that if "p" aliquots "m", then "p" can’t aliquot ,, …)

Solution. With induction on "i", we show that if "p" aliquots "", then for every, . We put.

If i=1, then  Now consider, So, .

14.15.9.1. Note

With this method of proof, you also can show that the number of prime numbers is infinite. Between this problem and previous problem there is a very close conceitedness. If "", be n-th Fermat’s number, simply can be showed that  that. You can adapt conditions of previous problem with this problem and show that if "p" be a prime number that aliquots "", then for every "i":

Because all of Fermat’s numbers are odd, so, every two different Fermat’s numbers are coprime. You can obtain the same results for quasi–Fermat numbers with some polynomial corresponding with them.

14.16. Problems concerning Fermat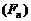, Mersenne,
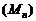perfect and redundant numbers

1. Always. (So, every composite Fermat’s numbers is quasi–prime).

2. Every Fermat’s number, except, is in  or  form.

3. Fermat’s numbers except "" and "" are ended to 17, 57, 37 and 97 regularly.

4. Calculate the number of digits of  in decimal.

5. Prove that Diophantine equation  exactly has an answer in natural numbers that .

6. Prove that 2¹⁷-1 is prime number.

7. Calculate smallest possible prime factor of 2¹⁹-1.

8. Suppose that "p" and "" two different odd prime numbers,  and . Prove that every odd prime divisor of  that doesn’t aliquot "", is in one of these form   or  or .

9. With thesis of previous problem, we consider that . Prove that  or "q" is in  form.

10.  Prove that  is prime.

11. Prove or disprove: Number  exists so that n! is perfect.

12. What is the first even perfect number greater than 10¹⁶ ?

13. What are the two last digits of perfect number of?

14. Prove or disprove: If be prime number, then:

is a perfect number.

15. Prove that if last digit of a perfect number be "8", then two last digits of it, is "28".

16. Prove or disprove: if "r", "s" and "t" be even perfect number and different, then:

17. Show that is a power of "2", if and only if "n" be in below form that and "" are Fermat's prime numbers and different:

18. Prove for every  ,"n" and "" are coprime.

(Hint. using this result that every prime division of is in form).

19. We call correct number  as redundant, if.

A. Find smallest redundant odd number (At first it seems that this number doesn’t exist).

B. If "n" be redundant, show that every positive coefficient of "n" also is redundant.

20. Find greatest common divisor of  and .

14.16.1. Note. Let  and. The list of all known primes p of which is a Mersenne prime, Therefore  is a perfect numbers.

Table of Known Mersenne Primes and perfect numbers

##	p (exponent)	Digits in	digits in	year		discoverer	notes
1	2	1	1	¾	¾
2	3	1	2	¾	¾
3	5	2	3	¾	¾
4	7	3	4	¾	¾
5	13	4	8	1456	Anonymous
6	17	6	10	1588	Cataldi
7	19	6	12	1588	Cataldi
8	31	10	19	1772	Euler
9	61	19	37	1883	Pervushin
10	89	27	54	1911	Powers
11	107	33	65	1914	Powers		note
12	127	39	77	1876	Lucas
13	521	157	314	1952	Robinson
14	607	183	366	1952	Robinson
15	1279	386	770	1952	Robinson
16	2203	664	1327	1952	Robinson
17	2281	687	1373	1952	Robinson
18	3217	969	1937	1957	Riesel
19	4253	1281	2561	1961	Hurwitz
20	4423	1332	2663	1961	Hurwitz
21	9689	2917	5834	1963	Gillies
22	9941	2993	5985	1963	Gillies
23	11213	3376	6751	1963	Gillies
24	19937	6002	12003	1971	Tuckerman		Tuckerman71
25	21701	6533	13066	1978	Noll & Nickel		NN80
26	23209	6987	13973	1979	Noll		"
27	44497	13395	26790	1979	Nelson & Slowinski		Slowinski79
28	86243	25962	51924	1982	Slowinski		Ewing83
29	110503	33265	66530	1988	Colquitt & Welsh		CW91
30	132049	39751	79502	1983	Slowinski
31	216091	65050	130100	1985	Slowinski
32	756839	227832	455663	1992	Slowinski & Gage		Peterson92
33	859433	258716	517430	1994	Slowinski & Gage
34	1257787	378632	757263	1996	Slowinski & Gage		(web page)
35	1398269	420921	841842	1996	Armengaud, Woltman, et. al. (GIMPS)		(web page)
36	2976221	895932	1791864	1997	Spence, Woltman, et. al. (GIMPS)		(web page)
37	3021377	909526	1819050	1998	Clarkson, Woltman, Kurowski et. al. (GIMPS, PrimeNet)		(web page)
38	6972593	2098960	4197919	1999	Hajratwala,Woltman,Kurowski et. al. (GIMPS, PrimeNet)		(web page)
??	13466917	4053946	8107892	2001	Cameron,Woltman, urowski et. al. (GIMPS, PrimeNet)		(web page)
??	20996011	6320430	12640858	2003	Shafer, Woltman, Kurowski et. al. (GIMPS, PrimeNet)		(web page)
??	24036583	7235733	14471465	2004	Findley, Woltman, Kurowski et. al. (GIMPS, PrimeNet)		(web page)
??	25964951	7816230	15632458	2005	Nowak, GIMPS et. al.		(web page)

We put question marks instead of a number for the last of the Mersenne primes because it will not be known if there are other Mersenne's in between these until a check and double check has been completed by GIMPS. See the GIMPS Status Page for more information. Note all smaller exponents have been tested.

[1]. In assertion in October of 1903, in American mathematics society, "Cole" was   going to deliver a lecture. Title of lecture was "decomposition of great numbers". After he invited to start the lecture, he went by the black board and without any speaking. He gave "2" to power "67" and subtracted one from out come. Then on other side of board, multiplied 761838257287 and 193707721 and result of two calculations was equal. Then he came back to his seat without any word later. He said to one of his friend that he spent "20" years of his life in every Sunday’s afternoon for finding the factors of "M₆₇".

[2] .For more information look at the table of known Mersenne prime and perfect numbers in the next pages.