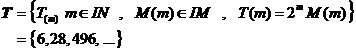CHAPTER 15

Definition of the sets of Fermat, Mersenne, perfect prime numbers by the prime numbers formula ""

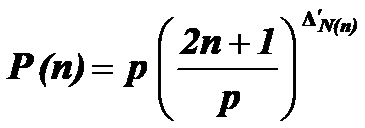
Definition of the set of Fermat's prime numbers  

15.1. Some general facts concerning Fermat’s numbers ()

 Fermat’s numbers are in "" form with below formula:

             (1)

First five terms of Fermat’s numbers sequence are:

           (2)

that all of them are prime numbers, Fermat thought that all of (1) numbers are prime numbers, but Euler in 1732 proved that "" is composite, because:

Two "" factors are prime number and therefore Fermat’s guess disproved it. Till now, prime number except (2) numbers don’t find in Fermat’s numbers. And most people guess that sequence of Fermat’s prime number is finite. Some other guesses that rareness of prime numbers in Fermat’s numbers is because of increasing speed of these numbers.

15.2. Definition of the set of Fermat’s prime numbers
by the prime numbers Formula

 If we consider  as a prime number:

 ;

                (3)

According to relation (3), set of Fermat’s prime numbers define:

(Set of Fermat’s prime numbers)

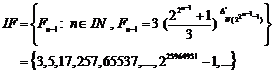
It is guessed that set of Fermat’s prime number (IF) is finite. Considering a kind of factorization of "" by previous Fermat’s numbers, this guess becomes stronger:

15.3. Some general facts about Mersenne's numbers and
even perfect numbers and the relation between them

Reviewing the Euclid's theorem and Euler’s theorem, existing infinite even perfect numbers is equal with existing infinite prime numbers in "" form. These kinds of prime numbers are called as Mersenne’s prime numbers. After this French monk in 17-th century, searched about these numbers, these numbers are famous as this name.

15.3.1. Definition

Consider that "n" be a positive correct number. n-th Mersenne’s number is correct number . If  be a prime number,  called as a Mersenne’s prime number. Trying to factorization the Mersenne's numbers, Fermat showed that if "p" be prime, then every prime divisor of "" has residual "1" in dividing by "p".

15.4. Definition of the sets of Mersenne, even perfect

        prime numbers by the prime numbers formula

If we consider the odd number  as a prime number:

 ;

                (1)

According to relation (1), set of Mersenne’s prime numbers is defined as below:

(Set of Mersenne's prime numbers)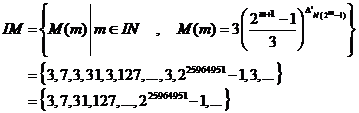

We know that with obtaining a new Mersenne’s prime number, we obtain a new perfect number. Because general formula of these even perfect numbers is:

              (2)

According to formula (2) and set of Mersenne’s prime numbers, set of even perfect number is defined as:

(Set of even perfect numbers)