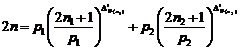CHAPTER 16

On the history of attempts for proving

Goldbach and Hardy conjectures

16.1. Goldbach and Hardy’s conjectures

In 1742, Goldbach wrote in a letter to Euler:

"It seems that every even number greater than 2 can be written as sum of two prime numbers". This claim of Goldbach is famous as Goldbach’s conjecture. In recent 250 years, Goldbach’s conjecture was subject and principle of extension researches. Hardy, famous English mathematician, stipulated that Goldbach’s guess is one of complicated unsolved problems of mathematics.

16.1.1. Goldbach’s conjecture

 Every even correct number, greater than "2", can be written as sum of two prime numbers. Numeral calculations verify validity of this guess and with a lot of method, we can write even numbers as sum of two prime numbers, although this number is big sufficiently. This conjecture had proved for all of numbers to 2.1015.

In 1973, Chen showed that big sufficiently even numbers can be written in  form that "p" is a prime number and "m" is a prime number or multiplication of two prime numbers. Goldbach guessed that every odd number greater than "7" can be written as sum of three prime numbers. Although this problem is open yet. But Vinogradov (1891-1983) showed in 1937 that all of great positive odd numbers can be written as sum of three odd prime numbers. In fact, it has been shown that Vinogradov’s result is established for every number greater than "". But in theoretical aspect, results must be verified on all of positive odd numbers. However, even if we use the fast modern calculators, then proving this result is impossible, because has "7" million digits.

16.2. Goldbach’s conjecture and other open problem related to it

16.2.1.

Show that Goldbach’s conjecture contains this subject that every odd correct number greater than "7" is sum of three odd prime numbers.

Solution. If "n" be an odd number greater than "7", then  is even and greater than "4", therefore, according to Goldbach’s conjecture  is sum of two prime number "p" and "q" more over, "p" and "q" are odd.

Because "4" is sum of two even prime numbers, so  is sum of three odd prime numbers.

16.2.2.

 According to Vinogradov’s theorem, every odd number great sufficiently is sum of three odd prime numbers. With help of this theorem, prove that every correct number great sufficiently, is sum of maximum four prime numbers.

Solution. With help of Vinogradov’s theorem, we show that every even number great sufficiently is sum of four prime numbers. Consider that we choose even number "n" such great that  is sum of three odd prime numbers "p", "q" and "r". So, and .

16.2.3.

Prove that Goldbach’s conjecture is equal with below sentence:

"every correct number  is sum of three prime numbers".

Solution. At first, consider Goldbach’s conjecture be correct. We show that every correct number  is sum of three prime numbers. If  be even, then "" is even and at least is equal with "4".

Therefore "" is sum of two prime numbers "p" and "q". So,  is sum of three prime numbers. If  be odd, then "" is even and at least equal with "4". So"" is sum of two prime numbers.

Therefore "n" is sum of three prime numbers. Now, consider that every "" be sum of three prime numbers. We show that Goldbach’s conjecture is correct. Consider  be even. So "" is sum of three prime numbers. But because "" is even, so at least one of these numbers must be equal with "2" (If all of three numbers be odd then "" will be odd). Therefore,  that "p" and "q" are prime numbers, so  is sum of two prime numbers.

16.2.4.

Prove that Goldbach’s conjecture need to this assertion that every odd number is in "" form and "n" is a natural number.

Solution. It is clear that ,  and . We consider that and . So, "" is even and greater than "6", then, two different prime numbers like "p" and "q" exist so that . It is clear that .

16.2.5. Historical remark

Although a lot of researched has been done about Goldbach’s conjecture this conjecture, generally, isn’t proved or disproved. But from these mentioned researches, important results are obtained that the most famous of them is Vinogradov’s works that in 1937 with plosive skill proved that "After on order, every odd number is sum of three odd prime numbers". This theorem has been origin of other research’s that beside them, other problem’s had been solved. In 1938-1940, N. Pipping directly verified validity of Goldbach’s conjecture for even number not more than 100000 and also showed all of odd numbers from "9" to "360749" as sum of three odd prime numbers that one of them is 3,5 or 7.

In 1966, Chen Jing- Run, Chinese mathematician, proved that every even number which is great sufficiently is sum of a prime number with a natural number that terminating has two prime factors. Below conjecture is stronger form of Goldbach’s conjecture.

16.2.6. (I). Goldbach’s conjecture (stronger form)

Every even number greater than "6", is sum of two different odd prime numbers. "Validity of this conjecture has been proved by calculation for odd numbers smaller than "". It is proved easily that every natural number greater than "6" is sum of different prime numbers.

16.2.7. (II). Hardy’s conjecture

Every even number is subtraction of two prime numbers (Hardy and Littlewood, 1923). Kronecker, issued this assertion that every even number can be written in infinite different method as subtraction of two odd prime numbers. Specially infinite twin prime numbers exist. (Of course Kronecker didn’t present a proof for this his claim). Although, still, any demonstration doesn’t present for this conjecture, but numeral calculations prove its validity. In fact, this problem can be propounded that infinite triplet prime numbers exist.  It means, infinite prime numbers "p" exist that "p" and "" and "" are prime. It is clear that only successive odd prime numbers are 3, 5 and 7.

16.3. Some unsolved problems and other conjectures               concerning prime numbers

In prime number theory there are a lot of unsolved problems and conjectural assertions that we have mentioned some of them before. Below assertions are other famous assertions that have not been proved or disproved yet. In solving problem, reeling upon these assertions, isn’t permitted. If its contrary stipulated.

III. Set of prime numbers in form of "" is infinite.

16.3.1. Remark about conjecture (III)

It is necessary to know that infinite prime numbers in below forms exist.

(A) , (B) , (C)

This assertion about (B), proved by Berdihin Russian mathematician in 1962. Its proof is very hard and difficult.

IV. At least one prime number exists between every two successive perfect square.

V. Every odd number not less than "9" is sum of three odd prime numbers.

VI. After an order, every natural number is perfect square or sum of a prime number with a perfect square.

16.3.2. Remark about guess (VI)

This conjecture belongs to Hardy and Littlewood (1923). Assertion isn’t established for all of natural numbers. For example 34 and 58 don’t justify in it.

Below questions are some of many questions that any answer didn’t find for them yet.

VII. Is the number of pairs of twin prime, infinite?

VIII. Is set of Mersenne’s prime numbers infinite?

IX. Is set of Fermat’s prime numbers infinite?

X.  For assumed natural number "a" is the set of prime numbers in "" form infinite.

XI. For every non-one natural number "n" is there any prime number between "" and ".

XII. Is set of prime numbers that their digits in decimal are equal with "1" infinite?

16.3.3. Remark about question( XII )

"11" is prime number and the 23-digit number of  is also prime that all of its digits are equal to "1". It is clear that in order to a number which all of its digits are equal to "1", be prime, necessary condition is the number of its digits be prime but this condition isn’t sufficient.

For example:

111=3.37, 11111=41.271, 1111111=239.4649

All digits of  that have "641" digits are "1" but it is divisible by 1283.

 

XIII. Sirpinski’s conjecture ("P conjecture" (1958)):

 For, we adjust natural numbers from "1" to "" in a "" table:

 

        1

       2

      3

   

   

  

       …

      …

      …

…

      …

 

"P" conjecture is that in every row of this table a prime number exists.

16.4. Applied investigations into Goldbach and Hardy conjectures

For examination of the conjectures of Hardy and Goldbach, we can use the formula of prime numbers:

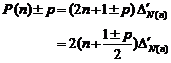
16.5. Theoretical investigation into Goldbach conjecture

Conjecture of Goldbach is equal to below conjecture:

"Every natural number greater than unit is arithmetic average of two prime numbers: "

It is obvious that as "m" becomes great, the number of answers become more. Here we suppose three possible cases:

I. If "m" be prime. The question is proved:

II. If "m" be an even number, it is obvious that prime numbers exist with "" (odd) distances from it. With to increase of "m", the number of answers will increase:

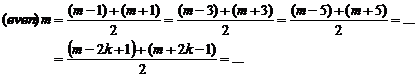
III. If "m" be an odd number, it is obvious that prime numbers exist with  (even) distances from it. With to increase of "m", the number of answers will increase:

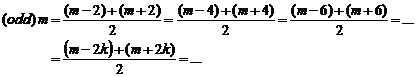
The number of recent equalities is equal to the number of prime numbers before "m", that according to the number of existing prime numbers in two successive intervals, Goldbach’s conjecture becomes near to true. In the other hand, if:

Then:

We suppose   ,      ;    then:

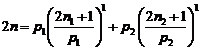
According to:

Result: