CHAPTER 17
On the history of attempts for proving the conjecture
of existence of infinity many twin prime numbers
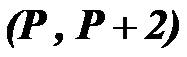
17.1. Twin prime numbers
17.1.1. A. De Polignac's conjecture
The problem of twin prime numbers depends on a conjecture,
famous as "A. De Polignac’s conjecture" that has 100 years record and
it is that if "k" be an arbitrary natural number, in sequence
of prime numbers , infinite successive pairs like "
" and "
" exist
so that "
".
I. It is clear that three prime numbers in form of p, 
and 
don’t exist
only for "
". But three numbers of
prime numbers exist in "p", and 
form, like prime
numbers 5, 7, 11. Such three prime numbers are called a prime triplet. One of
the greatest known triplets is:
10014491, 10014493, 10014497
Four prime numbers in p,, and 
form are called as
prime quartet. The first six prime quartets are obtained for:
p = 5, 11, 101, 191, 821, 1481
Some great prime quartets are as follow(
):
294311, 294313, 294317, 294319 ;
299471, 299473, 299477, 299479
We don’t have too much information about distribution of prime triplets and quartets.
II. In a quartet,"
p , "
and also " , " are twin, but some paris
of twin exist that no prime number separates them from each other but they
don’t form quartet like twin pairs (419, 421) and (431, 433).
Three twins also exist that no prime number separates them
like (179,181),
(191, 193) and (197, 199). There isn’t any prime number between 181 and 191 and
also between 193 and 197. At last, we know below quartet from prime twins and
with the same property:
(9419, 9421), (9431, 9433), (9437, 9439), (9461, 9463)
17.2. Clement’s theorem (1949)
We suppose that "n" be a non-one
natural number. If and only if "n" and "
" be a
prime twin, then:
.
17.3. Approaching to the solution of problem of infinity many twin prime numbers
In 1737, Euler proved that sum of 
that is added on prime
numbers, is infinite. An interesting method for approaching to problem of many
twin prime numbers is following sum:
17.4. The distances of prime numbers
Different questions are propounded about distances of prime numbers. It is clear that except 2 and 3, any two successive natural numbers do not exist so that both of them are prime number. More over, some sequence of natural numbers exists as long as we want that none of its term is prime.
17.4.1. Remark
Twin prime numbers namely pairs of prime numbers that their difference is "2", exist (Like (3,5) , (5,7) , (11,13) , (17,19)).
It is clear with calculating that the number of prime twins less than 105, 106 and 3.107, are respectively 1224, 8164, 152892.
In 1972, apparently the pair 76.3139 –1 and 76.3139+1 was the greatest known prime twin, but even in some references of 1974, 1012 +9649 and 1012+9651 is known as the greatest prime twin. There are only "20" prime twins between 1012 and 1012+10000. From this, some bodies have estimated that prime twins become rare as they become greater.
According to new researches and calculations, it is guessed that set of prime twins is infinite, but this guess is not proved or disproved till now.
17.5. Definitions and notes
It has been conjectured (but never proven) that there
are infinitely many twin primes. If the probability of a random integer "m"
and the integer 
being prime were statistically
independent events, then it would follow from the prime number theorem
that there are about 
twin primes less than or equal
to "m". These probabilities are not independent, so Hardy and
Littlewood conjectured that the correct estimate should be the following:
Here the infinite product is the twin prime constant (estimated by Wrench and others to be approximately 0.6601618158...) and we introduce an integral to improve the quality of the estimate. This estimate works quite well! For example,
the number of twin primes less than N:
|
N |
actual |
estimate |
|
|
8169 |
8248 |
|
|
440312 |
440368 |
|
|
27412679 |
27411417 |
There is a longer table by Kutnib and Richstein available online.
In 1919 Brun showed that the sum of the reciprocals of the twin
primes converges to a sum now called Brun's Constant (Recall that the sum
of the reciprocals of all primes diverges). By calculating the twin primes
up to 
(and
discovering the infamous pentium bug along the way). Thomas Nicely
heuristically estimates Brun's constant to be "1.902160578".
Twin primes table
|
rank |
Twin Primes |
digits |
who |
when |
|
1 |
33218925. |
51090 |
g259 |
2002 |
|
2 |
60194061. |
34533 |
g294 |
2002 |
|
3 |
1765199373. |
32376 |
g182 |
2002 |
|
4 |
318032361. |
32220 |
p100 |
2001 |
|
5 |
1807318575. |
29603 |
g216 |
2001 |
|
6 |
665551035. |
24099 |
g216 |
2000 |
|
7 |
1046886225. |
21082 |
p146 |
2004 |
|
8 |
1940734185. |
20012 |
g336 |
2004 |
|
9 |
781134345. |
20011 |
p53 |
2001 |
|
10 |
1693965. |
20008 |
g183 |
2000 |
|
11 |
83475759. |
19562 |
g144 |
2000 |
|
12 |
37831341. |
18605 |
g277 |
2003 |
|
13 |
1014561345. |
18434 |
g326 |
2004 |
|
14 |
291889803. |
18098 |
g191 |
2001 |
|
15 |
4648619711505. |
18075 |
IJW |
2000 |
|
16 |
2409110779845. |
18075 |
IJW |
2000 |
|
17 |
47280435. |
16361 |
g389 |
2005 |
|
18 |
488162409. |
16064 |
p135 |
2004 |
|
19 |
332494785. |
15395 |
g344 |
2004 |
|
20 |
168030135. |
15395 |
g344 |
2004 |
17.6. Problems concerning twin prime numbers
1. Prove that in a prime twin different from the pair 3 and 5, the smaller number is congruent with "5" with module "6".
2. Prime twin 5 and 7 have this property that numeral average of its numbers, namely "5" and "7", is a triangular number. Is there another prime twin with the same property?
3. Prime twin of previous question has is property that numeral average of its members is a perfect number. Is there another prime twin with the same property?