CHAPTER 18
Decisive solution to the problem of infinity many twin prime numbers and method of generating them and definition of twin prime numbers set by twin prime numbers formula
18.1. Generation of twin prime numbers
According to theorem of prime numbers production:
"Set of prime numbers is formed from cycles in below form:
We show easily that every new prime twin pair is produced from previous prime twin pairs.
For example, new prime twin pairs are produced from base
prime twin pairs namely (5,7) by adding the constant number
:
1. 
2. 
3. 
4. 
It sounds that three new greater prime twin pairs are produced from pair of base prime twin (5,7):
(11,13), (17,19), (29,31)
Therefore, in first cycle of prime numbers, there is one prime twin pair and the second cycle of prime numbers has three prime twin pairs that can be written as below:
Third cycle of prime numbers is in "
" form that the
next prime twin pairs will be produced with below method:
4.
5.
(In the first pack of third cycle, two prime twin pairs are produced)
6.
(Second pack, one twin pair)
7. 
8. 
(Third pack, two twin pairs)
9. 
10. 
(Forth pack, two twin pairs)
11. 
(Fifth pack, one twin pair)
12. 
13. 
(Sixth pack, two twin pairs)
Here, numeral sequences of prime twin pairs are produced regularly from three pairs of prime twin:
(11,13) : (30+11,30+13),( 60+11,60+13),(90+11,90+13),(180+11,180+13)
(17,19) : (90+17,90+19),(120+17, 120+19),( 180+17,180+19)
(29,31) : (30+29,30+31),(120+29, 120+31),(150+29, 150+31)
Therefore, ten new prime twin pairs are produced that every
one can be a generator for new twins. Attend that after the cycle 
, the twin
pairs (5, 7) has no role in producing the
new twins, because 
=1, 
and also twin pair (
11,13) from the next cycle will have no role in producing the new twins,
because
and
in the same method, base twin pairs produce new twins and themselves become
deleted in next cycle. In fact every base twin is substituted by some new twin
pairs.
Same method, in forth cycle, base twin pairs produce new prime twins as below:
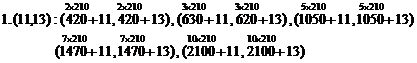
(From the first pack to tenth, five new prime twin pairs)
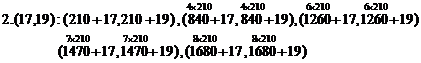
(From first pack to tenth, five new prime twin pairs)
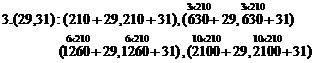
(From the first pack to tenth, four new prime twin pairs)
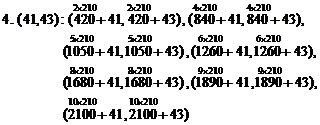
(From the first pack to tenth, seven new prime twin pairs)
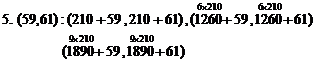
(From the first pack to tenth, three new prime twin pairs)
(From the first pack to tenth, only one new prime twin)
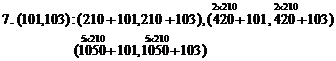
(From the first pack to tenth, three new prime twin pairs)
(From the first pack to tenth, two new prime twin pairs)
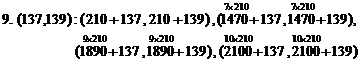
(From the first pack to tenth, four new prime twin pairs)
(From the first pack to tenth, two new prime twin pairs)
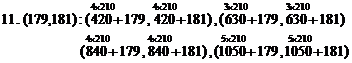
(From the first pack to tenth, four new prime twin pairs)
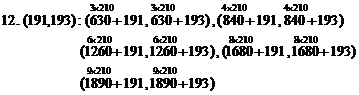
(From the first pack to tenth, five new prime twin pairs)
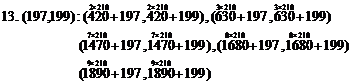
(From the first pack to tenth, five new prime twin pairs)
Therefore, obtained twins from third cycle are:
1. (11,13) :(431,433), (641,643) (1061,1063),(1481,1483) , (2111,2113)
2. (17,19) : (227,229), (857,859), (1277,1279), (1487,1489), (1697,1699)
3. (29,31) : (239,241), (659,661), (1289,1291), (2129,2131)
4. (41,43) : (461,463), (881,883), (1091,1093), (1301,1303), (1721,1723),
(1931,1933), (2141,2143)
5. (59.61): (269,271), (1319, 1321), (1949,1951)
6. (71,73): (281,283)
7. (101,103): (311,313), (521,523), (1151,1153)
8. (107,109): (1787,1789), (1997,1999)
9. (137,139): (347,349), (1607,1609), (2027,2029), (2237, 2239)
10. (149,151): (569,571), (1619,1621)
11. (179,181): (599,601), (809,811), (1019,1021), (1229,1231)
12. (191,193): (821, 823), (1031, 1033), (1451, 1453), (1871,1873),
(2081, 2083)
13.(197,199):(617,619),(827,829),(1667, 1669),(1877,1879),(2087,2089)
18.1.1. Remark
Some of the number of new twins is in 
form:
18.1.2. Remark
Some new prime twins are produced from successive numbers pair, for example (209,211).
According to the definition, we call these pairs of successive numbers that produce prime twin pairs, as "twin pairs maker".
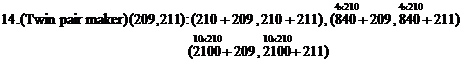
Twin pair maker (209, 211), produces three new prime twin pairs:
(209,211): (419, 421), (1049, 1051), (2309, 2311)
Twin pair maker (167,169) produces two new prime twin pairs:
Therefore, the number of prime twins in interval (210, 2311] is equal to "54" that "5" pairs of them have been produced from two twin pair makers.
18.1.3. Result
Growing of twins in any cycle is very slower than the previous cycle. Because from prime twin pairs of the first cycle produces three prime twin pairs and from three prime twin pairs of second cycle produce ten pairs of twin and from three prime twin pairs with addition ten prime twin pairs of third cycle produce "49" prime twin pairs. Ratio of twins of one cycle to the number of previous twins that are produced from them is:
It sounds that as we search more about prime twins in new cycles, with slow growing, the number of prime twins in very far cycles and in very extensive intervals tends to a very great number and it tends to infinite in infinite far cycle.
For example, the ratio of prime twins smaller than 
and
(1224, 8164,
152892) is:
18.1.4. Final Result
Since every prime twin pair with a cycle coefficient 
are located
in intervals that include some prime numbers, It is obvious that every prime
twin pair produces one pair of prime twin or at least one twin maker. So in every
cycle, some twin pairs or twin pair makers will be produced at least. Since
this phenomenon is repeated in every cycle, it is obvious that every prime twin
pair are produced unlimitedly and set of twins is infinite. We prove this
assertion in follow.
18.2. There is infinity many twin prime numbers
Proof. We know that every odd prime number greater
than "3" is in 
general form, because residue
"1" or "5" will be obtained from dividing of every prime
number by "6". It means every odd prime number is in "
" or
"
"
forms. On other side:
According to the table of
composite numbers, it is clear that odd composite numbers are obtained from
below numeral progressions:
(1)
It is obvious that if numbers in forms of "
" aren’t
in any form of above progressions, always a prime number will be obtained.
Therefore, If we delete all odd composite numbers in form (1) from numbers in general form,
number p (n) always is prime. In order to this, it is enough to solve
Diophantine equations in below general form and determine "n" with
respect to "k" and "p".
(2)
For example, we solve some equations and then we obtain general rule and sufficient conditions for solving the problem.
18.2.1. Example
General equation (2) makes the
conditions "
"for "n" in
case 
.
Because:
Therefore, in order to the numbers in form are not multiples
of "5", it must be "
".
18.2.2. Example
General equation (2) makes the conditions 
for "n"
in case p=7. Because:
Therefore, in order to the numbers in form are not multiples
of "7", it must be "
".
18.2.3. Example
General equation (2) makes the conditions 
for "n"
in case 
;
because:
Therefore, in order to the numbers in 
form aren't multiples
of "11", it must be 
as the same method.
18.2.4. Result
In order to the numbers in form of aren’t multiples of
prime "p", it must be:
(3)
18.3. Set of prime twin pairs
Since prime twin numbers are in 
form except of (3,5),
therefore, with conditions (3), set of prime twin numbers greater than
"3" are infinite and is in below form:
(Set of prime twin pairs) T
So:
T 
18.3.1. "H.M" Theorem.
If
and 
then 
is twin number.