CHAPTER 2

On the history of forming prime numbers tables and determining the smallest divisor of composite numbers

2.1. 2.1. Famous tables of prime numbers and divisors of                 composite numbers

Considering the importance of recognition the prime numbers and factorization numbers to them and in other side, difficulties of recognition of primality and factorization, some tables (of course restricted) of prime numbers and divisors or the smallest divisor of the composite numbers has been prepared. Some of the most famous of these tables are:

Lehmer, D.N; Table of factors for the first ten millions numbers containing the smallest factor of every number not divisible by 2,3,5 and 7 between the limits "1" and "10,017,000" list of prime numbers from "1" to 10,006, 721[1].

Kulik, J. ph. Poletti.L and Porter. R. list of prime numbers of 11-th million (precisely: from 100006741 to 10999997)[2].

Preparing the prime numbers table and the table of factors have old antecedent. In chapter "5" of the book "Arithmetic" by Fibonacci (1202) a list of prime numbers from "11" to "97" has been given, and also he mentioned the factorization of numbers 12-100 to their factors. Cathaldy provided a table from the prime numbers smaller than 750 in his research about perfect numbers. Then the bigger tables had prepared gradually. Some characteristic of some of the most important tables are presented in the next page, except 3 tables that has been mentioned at the first[3].

Tables of Divisors

Divisors table	Date	Provider
1-2,856,000	1785	Felkel
1-3,000,000	1817	Burkhard
7,000,000-9,000,000	1863	Dazet
1-100,000,000	1867	Kulik
3,000,000-6,000,000	1883	Glishare

The propounded tables are based on the Burkhard, Kulik, Glishare and Dazet works. Preparing the big tables is very tedious and needs a big patient,
attempt, tolerance and every body who looks at these tables, couldn’t restraint admiring the persons who has done this difficult job with no reward. Biller in his book "Entertainments in number theory" said "with seeing the attempt ion in this disordered world with war and continual conflict, it seems that the person who endowed the big part of their life to this work, must have found the secret of calmness and peace, that no wordily greedy person’s can reach it absolutely". Antonio Felkel, whose name was mentioned in the previous pages, in 1776, computed divisors of all numbers up to 2,000,000. The first part of his table (up to 408000) was printed by the Vian’s royal treasury but hadn’t costume and in the Austria war with Turkish, was used for preparing cartridge. Felkel was planning to take back the rest of his table, but the treasury refused and since he disappointed to gain it, again he computed the divisors of the numbers from 408000 to 2856000. Philip Kulik’s motivation in preparing the factor’s tables is in conceivable. He had prepared this table lonely in 2o years. Lehmer verified the first volume of these 8 volumes in Royal academy in Wiena and described it in the preface of factor’s table with enthusiasm and anxiety so that impresses the readers. The Kulik’s table was used in preparing the table of "Kulik, Poletti and Forter" that we have mentioned before, and reformed its mistakes.

2.2. 2.2. Calculation of tables

According to our previous statements, it is clear that easily but with patience, it’s possible to prepare the table numbers.

In fact, it took long many years to determine the prime numbers smaller than 10 million. These tables are printed and for each of the first 10 million numbers, the smallest odd divisor was written in front of them. Therefore, each number that nothing is written in front of it (has no divisor), it is prime number. Also some others have calculated the prime numbers between two big numbers (bigger than 10 million) for example, the prime numbers between 100,000,000 and 100,100,000. It is clear that these calculations are very detailed and long, because all numbers between these two numbers that are multiplicand of prime numbers smaller than approximate square root of 100 million should be omitted.

(It means the smaller prime numbers less than 10,000 that are nearly 2000 numbers).

Extension and completing the calculators help to speed of calculations. However it must be knotted to prevent the mistake of copying, and printing.

It is expected, this valuable work helps to improvement our knowledge about prim numbers greatly and this analysis (that we can’t explain it, in this book).

However we must confess, there are a lot of ambiguous points despite so many attempts to recognition the prime numbers. But with patient researches that done about the prime numbers tables, it seems that some of these theorems will be confirmed by the mathematician’s reasoning. No doubt that this experimental and sensuous method, by some of the mathematician has been ursine successfully. And here, it isn’t un-useful to present some of the researches to cleat the prime numbers recognition category.

2.3. 2.3. Stochastic’s Theorem

One of the most attractive theorems that are resulted from these statistic researches is stochastic theorem. This theorem has perfect relation with sieve alternation’s rule (that we have mentioned it before), But we can say that random theorem completes this rule in some cases.

It is clear that divisible numbers by prime divisors 2, 3 and 5 are repeated in every 30 successive numbers frequently. The numbers not divisible by 2, 3 and 5 are in one of below form:

30n+1              30n+7              30n+11

30n+13                        30n+17                        30n+19

30n+23                        30n+29                       

(Or: , ).

In the first ten numbers, There are two numbers and in the second ten numbers, four and in the third ten numbers, there are two numbers of these.

In this numbers, there are 26 numbers that are between "1" to "100" and 28 numbers between 101 to 200 and 26 numbers between 201 to 300 and these numbers are repeated successively in every next 100 numbers in this way.

Now, if we consider the prime numbers between 2 to 13, their multiplications are equal or 30030. Here again the same procedure is repeated but succession period is equal to 30030 instead of 30 and also if we devoid successive numbers to the packs containing 30 numbers, (the packs that have 8 un-divisible number by 2 and 3 and 5), the number of numbers that are divisible by 7, 11, 13 in these patches will be various. For the first ten packs (1 to 30 and 31 to 60 and … and 271 to 300) the numbering of these numbers are 3,1,1,2,3,2,3,2,3,1,... and in this way the number of numbers that are not divisible by 2,3,5,7,11,13 will be equal to 5,7,7,6,5,6,5,6,7 (that are calculated  from subtracting the previous values of 8). By the same way, various values will be calculated for the first 1001 packs of the 30 number namely up to 30030.

Only when we reach to this number, the previous values will be repeated prodigally. It means that there are 5 number between 30031 to 30060 that they are not divisible by 2,3,5,7,11,13 ( that equal the number of these numbers, when we consider the number between 1 to 30).

It seems that when want to increase the number of prime numbers, the length of succession period will grow rapidly. So if we want to search for the numbers that are not divisible by any of smaller prime numbers than 100, the succession period will be equal multiplication of these number that is a number with 30 digits approximately, and it is clear that the periodic method can not be used neither for the numbers that their primality can be investigated nor for the numbers bigger than one million that their smallest prime factor is near to 1000.

Now we can explain the random theorem: it concerns the distribution of the prime numbers in the consecutive packs of numbers. For example the distribution in the packs of 100- numbers, follows the random theorem, with considering the succession period for the smaller prime numbers. This will decrease the numbering of the prime numbers which exist probably.

If we limit the factors to 2, 3, 5 there will be 26 or 28 number in every 100 successive numbers, so that they aren’t divisible by 2, 3, 5, and if we consider the factor 7 these number will even decrease. In other side it is possible to determine the average of the prime numbers which exist between every 100 numbers, for example the numbers between 1,000,000 and 1,100,000 and these numbers will be more than 7.

If the distributing of prime numbers were requited, there would be 7 prime numbers in every 100 number. But in fact despite the number 7 exist frequently, but the real number of prime numbers is often different from 7 in 100-number intervals and varies from 0 to 14.

Comparing the prime numbers with the obtained resorts, clarifies that in measure 100, in a box, there are 7 black balls in every 100 balls. It means 7 black balls and 93 white balls. It’s clear that difference of the number of prime numbers to their average is very less than the ratio that is shown here. Therefore, is necessary to pay attention to certain recurrence that is verified for small prime numbers.

The recurrence arranged this phenomenal. If we consider only prime factors 2, 3, 5, we will see that the number of numbers that are prime probably, (It means the numbers that are not divisible by 2, 3, 5) is equal to 26 or 28 in every recurrence 100 numbers. Therefore, is not necessary to consider a box with 100 balls. But we must consider a box for example which has 20 white balls against every 7 black balls (in measure 27 balls). It is possible to consider more prime numbers.

The multiplication of prime number up to 17 is equal to 510510 and up to 19 is equal to 9699690. The numbers which are under our consideration are between these two multiplications and if we consider prime number up to 17, another arrangement will be established. There are numbers between the first 510510 numbers that aren’t divisible by prime number up to 17.

It means that there are 576016 numbers between 500000 numbers and it will be %18 of them. Now we consider the balls in every 18 balls, 7 black balls and 11 white balls and it is verified that the ratio calculated by theoretical hypothesis is very closer to the observed conditions.

Now we can arrange random theorem:

We consider the pack "T" which is randomly chosen from the successive 100 numbers for example between 2,000,000 and 2,100,000. The probability that the pack "T" includes "p" prime numbers is equal to the probability of existing "p" black balls in "q" balls in a box that has "n" black balls and
"" white balls. The numbers "q" and "n" are selected in this way: the number "q" is the possible number of number which can be in every 100 prime numbers, in clouding the numbers that are divisible by small prime number (up to 17), and the number "n" is the average number of prime numbers which are in every 100 number of studied pack.

It is clear that it is not correct to speak about the primality of a supposed number, because if a number be determined, it is easy to determine that it is prime or not. But we can speak about primality of a number if it is selected randomly with some condition. For example suppose that the number of a lottery winner is a prime number.

Here we use classification pattern to shorten numerical tables.

The following table is designed for the interval (31,211]:
Note: The Composite numbers are bold.

	+30	+60	+90	+120	+150	+180	×	7	11	13
7	37	67	97	127	157	187	7	49
11	41	71	101	131	161	191	11	77	121
13	43	73	103	133	163	193	13	91	143	169
17	47	77	107	137	167	197	17	119	187
19	49	79	109	139	169	199	19	133	209
23	53	83	113	143	173	203	23	161
29	59	89	119	149	179	209	29	203
31	61	91	121	151	181	211

Ÿ Multiplication table determining composite numbers in the interval (31,211]

2.3.1. Note. To eliminate composite number from the table it suffices to form the multiplication table of the interval under consideration.

Considering the multiplication table for the aforementioned interval 12 composite numbers are obtained which are to be eliminated from the table associated with the cycle 30s+p.

For the interval (211, 2311] the table of classes is as the following:

(210,p) =1	+210	+420	+630	+840	+1050	+1260	+1470	+1680	+1890	+2100
11	221	431	641	851	1061	1271	1481	1691	1901	2111
13	223	433	643	853	1063	1273	1483	1693	1903	2113
17	227	437	647	857	1067	1277	1487	1697	1907	2117
19	229	439	649	859	1069	1279	1489	1699	1909	2119
23	233	443	653	863	1073	1283	1493	1703	1913	2123
29	239	449	659	869	1079	1289	1499	1709	1919	2129
31	241	451	661	871	1081	1291	1501	1711	1921	2131
37	247	457	667	877	1087	1297	1507	1717	1927	2137
41	251	461	671	881	1091	1301	1511	1721	1931	2141
43	253	463	673	883	1093	1303	1513	1723	1933	2143
47	257	467	677	887	1097	1307	1517	1727	1937	2147
53	263	473	683	893	1103	1313	1523	1733	1943	2153
59	269	479	689	899	1109	1319	1529	1739	1949	2159
	...	...	...	...	...	...	...	...	...	...
191	401	611	821	1031	1241	1451	1661	1871	2081	2291
193	403	613	823	1033	1243	1453	1663	1873	2083	2293
197	407	617	827	1037	1247	1457	1667	1877	2087	2297
199	409	619	829	1039	1249	1459	1669	1879	2089	2299
209	419	629	839	1049	1259	1469	1679	1889	2099	2309
211	421	631	841	1051	1261	1471	1681	1891	2101	2311

According to the tables, just mentioned, it follows that prime numbers are generated by the following general formula:

            (1)

In the above, is called the cycle constant and consider it to be equal to one of the numbers in the following sequence:

In (1) "p" is called the generating number. This definition justify adding a multiple of to "p" would result in new prime numbers. The positive integer depends on the cycle constant; i.e., if we consider the cycle constant as follows (is the prime number following)

The upper and lower bounds for are as follows:

We conclude that the set of prime numbers consists of a union of numerical cycles as described in (1). Each of these cycles is consisted of "n" numerical classes. The number "n" is in fact equal to the ratio of the distance of two consecutive cycles constant to the first one:

    (The number of classes)

According to this prime numbers could be regularized meaning that prime numbers associated with symbols "" or "" could be listed in a table with formulas of the form (1). For example, according to the former tables prime numbers of the cycle ,  for and could be written as follows :

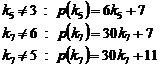
2.3.2. Note. If in case the number of prime numbers of classes in a cycle is larger, it's better to use the symbol "", otherwise, the symbol "" is used.

As another example the cycle,, for are as follows:

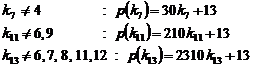
Here, the following table is used to regularize prime number. This table could be extended to any given arbitrary cycle.

Prime numbers table in terms of consecutive cycles.

Table of prime numbers (H.M)

5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67

71
73
79
83
89
97
101
103
107
109
113
121		F	F	F
127
131
137
139
143		F	F	F
149
151
157
163
167
169			F	F
173
179
181
187		F	F	F
191
193
197
199
209		F	F	F
211
221			F	F
223
227
229
233
...	...	...	...	...

2.3.3.Note This table gives any prime less than, i.e. .

The following table (I) is designed for the number that are divisible by prime numbers of classes:

a: "2" , "3" and "5".                     b: from "7" up to "19".

c: from "23" up to "97".              d: greater than "100".

e: prime numbers.

Table (I)

N	A	b	c	d	e	Error controlling
2000000+ 0001000 10001000 20001000 30001000 40001000 50001000 60001000 70001000 80001000 90001000	7334 7334 7332 7334 7334 7332 7334 7334 7332 7334	955 959 956 954 956 957 957 954 960 959	497 508 502 513 505 512 504 507 507 502	509 508 517 509 534 503 511 531 515 531	705 691 693 691 670 696 684 674 686 674	(+1) (-1)
summand	73334	9567	5057	5168	6874

For every column of this table, a table with move detailed is prepared that we show that for column e, namely the column of prime numbers, (table (II) in next page). Every row of this tables justify with a pack of 10000 numbers like every row of the previous table.

Table (II)

	1	2	3	4	5	6	7	8	9	10	11	12	13
0001000 10001000 20001000 30001000 40001000 50001000 60001000 70001000 80001000 90001000	2 1	2 2 1 2 2 2	3 3 5 2 2 3 4 5 2 3	7 8 9 4 8 5 6 7 9 5	13 10 9 14 13 10 12 13 9 15	25 20 13 17 26 23 25 14 17 17	10 22 23 25 14 23 18 23 25 22	13 17 15 22 11 13 12 16 18 20	16 15 11 4 11 12 11 14 11 10	10 2 8 6 11 7 7 3 3 6	2 1 5 3 1 3 3 3	2 1 2 2 1	1 1
summand	3	11	32	68	118	197	205	157	115	63	21	8	2

And this pack is divided to 100 packs of 100 numbers. The recorded numbers in various columns of the first row of this table, determine the number of prime numbers in packs of 100 numbers from these 100 packs (that started from 2000001). So there are three packs of these packs that every one includes 3 prime numbers. 7 packs include 4 prime numbers, 13 packs include 5 prime numbers. 25 packs include 6 prime numbers, 10 packs include 7 prime numbers, 13 packs include 8 prime numbers, 16 packs include 9 prime numbers, 10 packs include 10 prime numbers, 2 packs include 10 prime numbers, 2 packs include 11 prime numbers and at last one pack include 13 prime numbers and the next rows follow this order.

Investigating this table, show that some disorders exist in every row, about distribution of 100 numbers which include the number of prime numbers (from 1 to up 13), (average number that obtained from table (I) is 6.874).

First row has two maximum numbers (25 and 16).

Numbers of six-th column decrease unexpectedly for the rows 20001 and 70001 (13 and 14) and also in rows 00001 (10) and 40001 (14). But the seams show a kind of ordered distribution of prime numbers according to the first law of lap lass – gauss, with an important distribution when the number of prime numbers equals "1" in some packs of 100 numbers and in some other equals 13. But this distribution is result of the random that obtained for 1000 series, and probability of existing 17 prime numbers is in every series. Like a box which include 17000 balls that 6874 balls are black. The observed disorders are usual and it confirms the random theorem.

Now we search the obtained results from previous table, about 10000 packs of 100 numbers up to 10 million, namely numbers between 9000001 up to 10 million.

Table (III)

	n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
90 to 91 91 to 92 92 to 93 93 to 94 94 to 95 95 to 96 96 to 97 97 to 98 98 to 99 99 to100	6182 6245 6259 6223 6177 6271 6202 6208 6181 6134	1 1	4 2 2 3 6 1 3 3 1 4	21 20 26 21 24 13 25 17 15 21	54 60 48 53 56 54 55 60 67 65	124 126 98 103 105 124 111 122 113 104	176 151 161 161 189 157 176 173 180 188	186 195 228 215 200 194 212 197 208 209	179 189 190 195 166 206 170 167 178 178	131 127 127 114 120 139 112 133 119 115	82 78 77 73 84 59 83 68 70 67	32 29 24 24 41 32 34 40 28 33	9 15 12 12 6 10 14 17 15 10	2 6 6 3 3 8 4 2 3 5	2 1 2 2 1 2	1 1 1
summand	62082	2	29	203	572	1140	1712	2044	1818	1237	751	317	120	42	10	3

In the first of table (III) which is identified by , there are 100,000 units in every row, it means 1000 packs of 100 numbers, for example from  up to , then in column "n" the number of prime numbers of this interval is written, and in next columns that numbers from "1" up to "14" is written above them, the number of 100-number packs is identified which have "1" or "2",..., or "14" prime numbers. As it is found out from the sums, it seems that the distribution of prime numbers are arranged completely and almost, there is a result for 10 million like the same result for 3 million. Therefore, we can accept that a general rule exists.

It is surprising to use this statistics of the prime numbers about approximate distances, very big number like 100 million. The column is very interesting because it shows that how is the frequency of prime numbers near the indeterminate number "N". This column result that there is important diversity for big distances in relative to this theoretical frequency.

For distances of 100,000, the number of prime numbers that are in 10^th million is equal to:

6182                        6245                        6223                        6177
6271                        6202                        6201                        6134

It seems that the first number is very small abnormally, but its second root hasn’t big diversity in relative to average value so that it is possible to consider it as normal.

If we put 100,000 instead of 200,000, disordering will decrease so that if we add adjacent numbers two by two, will have:

12427, 12482, 12448, 12410, 12315

and with addition of three-to-three of these numbers (distances of 300,000):

18686                      18671                      18591                      (61314)

The obtained number will approach to each other continuously. Finally by adding           4-to-4 or 5-to-5:

24909                                      24858
31086                                      30996

2.4. 2.4. Another research on stochastic theorem

 Mr. Giuseppe Palama had presented and it led to searching about random theorem. The subject is definition of prime numbers in the form  and between 11000000 and 11100000.

Euler had shown that if integer number "n" chooses values, only numbers in  form are prime numbers. He had determined a lot of these values of "n" that the greatest of them is. This remark of Euler proves (Mr. Palama’s statistics), when he determined 23 prime numbers in  form between the numbers  and.

Also in every 100 packs of 1000 numbers there are in average 2.03 prime numbers with above form in distance 100000. We can determine easily number "N" that is indicator of the number of packs of 1000 numbers and include 0, 1, 2, 3, 4, 5, … prime numbers, so below table obtains:

Table (IV)

	0	1	2	3	4	5	6	7	8	summand
N…	7	25	38	23	3	4	0	0	0	100
Poisson	13.5	27.1	27.1	18	9	3.6	1.2	0.3	0.1	99.9

Also he mentioned a form of non – prime odd numbers in this distance but this form isn’t complete.

In third row, we have recorded the theoretical values resulted form Poisson’s relation.

It is clear that the concerned distribution proves the random rule. But it has more tendencies to a kind of arrangement in relation to random rule.

2.5. 2.5. Table of divisors of Burkhard

We express a skillful work from J.C.Burkhard in 1817 (divisors table), reprinted with permission from Gs. Carr from the famous book "Formulas and theorems in mathematics" (New York: Chelsea publishing company 1970) that it develops to "99000". This table calculates the least divisor of every integer number from "1" to "90000" that isn’t multiple of 2 or 3 or 5 (except prime numbers "P" which put O (Zero) against them).

 A skillful work form J.C.Burkhard in 1817 that reprinted by printed by Permission from Gs. Carr from the famous book “Formulas and Theorems in Mathematics” (New York: Chelsea publishing company 1970) you can see a part of this table in the next page.

Table (V)

	00	03	06	09	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60	63	66	69	72	75	78	81	84	87
01 07 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 83 89 91 97	0 0 0 0 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 7 0 0 0 7 0	7 0 0 0 0 11 17 7 0 0 11 7 0 0 0 0 19 0 7 0 13 0 0 0 17 0	0 0 13 0 0 0 7 17 0 7 0 0 0 11 0 0 0 23 11 0 0 7 0 13 0 17	17 0 0 11 7 0 13 0 7 0 0 23 0 13 0 7 31 0 0 7 0 11 0 23 0 0	0 17 7 0 0 23 0 0 0 0 17 11 29 0 7 0 13 7 31 19 0 0 0 0 0 0	19 11 0 17 37 7 0 11 0 29 23 0 7 0 0 0 7 0 0 11 19 0 0 7 37 0	0 13 0 7 23 17 0 31 0 11 7 19 0 43 17 11 0 0 0 0 0 0 7 0 31 7	11 7 0 0 29 13 11 0 0 0 0 0 19 7 0 17 0 11 13 41 7 0 37 11 7 13	7 29 0 19 0 41 0 7 11 0 0 7 0 31 11 0 23 0 7 0 0 37 13 19 47 11	37 0 0 0 11 0 7 0 0 7 0 13 41 0 0 31 11 0 17 47 0 7 11 0 0 0	0 31 0 23 7 0 0 13 7 0 0 17 11 0 43 7 0 0 37 7 17 0 0 0 11 19	0 0 7 0 31 0 0 0 0 47 13 0 0 17 7 0 0 7 0 0 11 31 17 0 0 43	13 0 23 0 0 7 0 19 0 0 11 0 7 41 13 0 7 19 0 0 0 13 29 7 0 0	47 0 0 7 0 0 0 0 0 31 7 0 0 11 59 37 17 0 11 29 41 23 7 0 13 7	0 7 0 11 0 0 41 0 0 19 0 0 31 7 0 0 0 17 0 0 7 11 0 0 7 0	7 0 13 0 0 0 0 7 23 13 19 7 0 0 29 47 0 0 7 17 23 19 0 13 0 0	0 11 17 0 0 61 7 11 0 7 47 29 37 13 23 43 0 31 0 11 0 7 19 0 67 59	0 0 19 0 7 0 47 23 7 11 53 37 0 19 0 7 13 0 0 7 31 0 71 0 29 0	11 0 7 0 0 0 11 61 0 0 0 0 13 0 7 53 43 7 0 13 0 0 0 11 17 23	0 13 0 29 0 7 59 17 11 0 0 0 7 0 11 13 7 73 29 23 53 0 0 7 0 11	17 0 6 7 11 13 19 0 37 0 7 0 0 23 0 73 11 0 13 0 59 0 7 0 0 7	0 7 0 59 0 71 0 0 13 0 17 0 11 7 0 0 0 0 23 0 7 0 13 0 7 0	7 0 11 17 13 0 37 7 19 0 29 7 17 61 0 0 0 59 7 0 11 0 41 0 0 37	67 0 0 31 0 11 7 13 29 7 11 53 0 0 17 0 0 0 0 19 0 7 0 29 0 0	19 0 0 0 7 0 31 0 7 0 13 0 0 11 0 7 53 13 11 7 19 29 0 37 23 0	13 0 7 11 0 73 0 0 17 0 0 19 0 0 7 0 0 7 67 0 0 11 0 0 0 71	29 37 73 13 0 7 0 0 41 17 0 11 7 47 0 29 7 0 17 0 0 0 0 7 13 53	0 11 0 7 0 23 0 11 47 79 7 17 0 29 31 41 0 0 0 11 13 0 7 19 0 7	31 7 13 47 19 0 0 0 0 11 23 0 0 7 79 11 0 0 43 37 7 61 17 13 7 29	7 0 31 0 23 0 11 7 0 0 0 7 0 13 0 19 0 11 7 31 67 0 0 11 59 19

	01	04	07	10	13	16	19	22	25	28	31	34	37	40	43	46	49	52	55	58	61	64	67	70	73	76	79	82	85	88
01 03 07 09 13 19 21 27 31 33 37 39 43 49 51 57 61 63 67 69 73 79 81 87 91 93 97 99	0 0 0 0 0 7 11 0 0 7 0 0 11 0 0 0 7 0 0 13 0 0 0 11 0 0 0 0	0 13 11 0 7 0 0 7 0 0 19 0 0 0 11 0 0 0 0 7 11 0 13 0 0 17 7 0	0 19 7 0 23 0 7 0 17 0 11 0 0 7 0 0 0 7 13 0 0 19 11 0 7 13 0 17	7 17 19 0 0 0 0 13 0 0 17 0 7 0 0 7 0 0 11 0 29 13 23 0 0 0 0 7	0 0 0 7 13 0 0 0 11 31 7 13 17 19 7 23 0 29 0 37 0 7 0 19 13 7 11 0	0 7 0 0 0 0 0 0 7 23 0 11 31 17 13 0 11 0 0 0 7 23 41 7 19 0 0 0	0 11 0 23 0 19 17 41 0 0 13 7 29 0 0 19 37 13 7 11 0 0 7 0 11 0 0 0	31 0 0 47 0 7 0 17 23 7 0 0 0 13 0 37 7 31 0 0 0 43 0 0 29 0 0 11	41 0 23 13 7 11 0 7 0 17 43 0 0 0 0 0 13 11 17 7 31 0 29 13 0 0 7 23	0 0 7 63 29 0 7 11 19 0 0 17 0 7 0 0 0 7 47 19 13 0 43 0 7 11 0 13	7 29 13 0 11 0 0 53 31 13 0 43 7 47 23 7 29 0 0 0 19 11 0 0 0 31 23 7	19 41 0 7 0 13 11 23 47 0 7 19 11 0 7 0 0 0 0 0 23 7 59 11 0 7 13 0	0 7 11 0 47 0 61 0 7 0 37 0 19 23 11 13 0 53 0 0 7 0 19 7 17 0 0 29	0 0 0 19 0 0 0 0 29 27 11 7 13 0 0 0 31 17 7 13 0 0 7 61 0 0 17 0	11 13 59 31 19 7 29 0 61 7 0 0 43 0 19 0 7 0 11 17 0 29 13 41 0 23 0 53	43 0 17 11 7 31 0 7 11 41 0 0 0 0 0 0 59 0 13 7 0 0 31 43 0 13 7 37	13 0 7 0 17 0 7 13 0 0 0 11 0 7 0 0 11 7 0 0 0 13 17 0 7 0 19 0	7 11 41 0 13 17 23 0 0 0 0 13 7 29 59 7 0 19 23 11 0 0 0 17 11 67 0 7	0 0 0 7 37 0 0 0 0 11 7 29 23 31 7 0 67 0 19 0 0 7 0 37 0 7 29 11	0 7 0 37 0 11 0 0 7 19 13 0 0 0 0 0 0 11 0 0 7 0 0 7 43 71 0 17	0 17 31 41 0 29 0 11 0 0 17 7 0 11 0 47 61 0 7 31 0 37 7 23 41 11 0 0	37 19 43 13 11 7 0 0 59 7 41 47 17 0 0 11 7 23 29 0 0 11 0 13 0 43 73 67	0 0 19 0 7 0 11 7 53 0 0 23 11 17 43 29 0 0 67 7 13 0 0 11 0 0 7 13	0 47 7 43 0 0 7 0 79 13 31 0 0 7 11 0 23 7 37 0 11 0 73 19 7 41 47 31	7 67 0 0 71 13 0 17 0 0 11 41 7 0 0 7 17 27 62 0 73 47 11 83 19 0 13 7	11 0 0 7 23 19 0 29 13 17 7 0 0 0 7 13 47 79 11 0 0 7 0 0 0 7 43 0	0 7 0 11 41 0 89 0 7 0 0 17 13 0 0 72 19 0 31 12 7 79 23 7 61 0 11 19	59 13 29 0 43 0 0 19 0 0 0 7 0 73 37 22 11 0 7 0 0 17 7 0 0 0 0 43	0 11 47 67 0 7 0 0 19 7 0 0 0 83 17 43 7 0 13 11 0 23 0 31 11 13 0 0	13 0 0 23 7 0 0 7 0 11 0 0 37 0 63 17 0 0 0 7 19 13 83 0 17 0 7 11

	02	05	08	11	14	17	20	23	26	29	32	35	38	41	44	47	50	53	56	59	62	65	68	71	74	77	80	83	86	89
03 09 11 17 21 23 27 29 33 39 41 47 51 53 57 59 63 69 71 77 81 83 87 89 93 99	7 11 0 7 13 0 0 0 0 0 0 13 0 11 0 7 0 0 0 0 0 0 7 17 0 13	0 0 7 11 0 0 17 23 13 7 0 0 19 7 0 13 0 0 0 0 7 11 0 19 0 0	11 0 0 19 0 0 0 0 7 0 29 7 23 0 0 0 0 11 13 0 0 0 0 7 19 29	0 0 11 0 19 0 7 0 11 17 7 31 0 0 13 19 0 7 0 11 0 7 0 29 0 11	23 0 17 13 7 0 0 0 0 0 11 0 0 0 31 0 7 13 0 7 0 0 0 0 0 0	13 0 29 17 0 0 11 7 0 37 0 0 17 0 7 0 41 29 7 0 13 0 0 0 11 7	0 7 0 0 43 7 0 0 19 0 13 23 7 0 11 29 0 0 19 31 0 0 0 0 7 0	7 0 0 7 11 23 13 17 0 0 0 0 0 13 0 7 17 23 0 0 0 0 7 0 0 0	19 0 7 0 0 43 37 11 0 7 19 0 11 7 0 0 0 17 0 0 7 0 0 0 0 0	0 0 41 0 23 37 0 29 7 0 17 7 13 0 0 11 0 0 0 13 11 19 29 7 41 0	0 0 13 0 0 11 7 0 53 41 7 17 0 0 0 0 13 7 0 29 17 7 19 11 37 0	31 11 0 0 7 13 0 0 0 0 0 0 53 11 0 0 7 43 0 7 0 0 17 37 0 59	0 13 37 11 0 0 43 7 0 11 23 0 0 0 7 17 0 53 7 0 0 11 13 0 17 7	11 7 0 23 13 7 0 0 0 0 41 11 7 0 0 0 23 11 43 0 37 47 53 59 7 3	7 0 11 7 0 0 19 43 11 23 0 0 0 61 0 7 0 41 17 11 0 0 7 67 0 11	0 17 7 53 0 0 29 0 0 7 11 47 0 7 67 0 11 19 13 17 7 0 0 0 0 0	0 0 0 29 0 0 11 47 7 0 71 7 0 31 13 0 61 37 11 0 0 13 0 7 11 0	0 0 47 13 17 0 7 73 0 19 7 0 0 53 11 23 31 7 41 19 0 7 0 17 0 0	13 17 31 41 7 0 17 13 43 0 0 0 0 0 0 0 7 0 63 7 13 0 11 0 0 41	0 19 23 61 31 0 0 7 17 0 13 19 11 0 7 59 67 47 7 43 0 31 0 53 13 7	0 7 0 0 0 7 13 0 23 17 79 0 7 13 0 11 0 0 0 0 11 61 0 19 7 0	7 23 17 7 0 11 61 0 47 13 31 0 0 0 79 7 0 0 0 0 0 29 7 11 19 0	0 11 7 17 19 0 0 0 0 7 0 41 13 7 0 19 0 0 0 13 7 0 71 83 61 0	0 0 13 11 0 17 0 0 7 11 37 7 0 23 17 0 13 67 71 0 43 11 0 7 0 23	11 31 0 0 41 13 7 17 0 43 7 11 0 29 0 0 17 7 31 0 0 7 0 0 59 0	0 13 11 0 7 0 0 59 11 71 0 61 23 0 0 0 7 17 19 7 31 43 13 0 0 11	53 0 0 0 13 71 23 7 29 0 11 13 83 0 7 0 11 0 7 41 0 59 0 0 0 7	19 7 0 0 53 7 11 0 13 31 19 17 7 0 61 13 0 0 11 0 17 83 0 0 7 37	7 0 79 7 37 0 0 0 89 53 0 0 41 17 11 7 0 0 13 0 0 19 7 0 0 0	29 59 7 37 11 0 79 0 0 7 0 23 0 7 13 17 0 0 0 47 7 13 11 89 17 0

This table calculates the least divisor of every integer number from 1 to 90000 that isn’t multiple of 2, 3 or 5 (except prime number  that put 0 in front of them). The first two digits of integer number (from left to right) are in row numbers from bold kind and the last two digits are in left column. For example:

[1]. Carnegie Institution of Washington Publication 105, 1909 (165, 1914)

[2]. From tables of manuscript, Amsterdam 1951

[3]. Historical subject of this part is based on the first volume of "History of theory of numbers" Dickson, "primary numbers" by Biller. Table in the next page is from the last book.