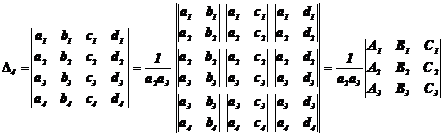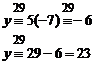CHAPTER 21
The newest of methods of solving and calculating
Appendixes (I)
Contents
Ÿ Solving congruence and Diophantine equations by "H.M" table (New Method):
Ÿ Solving Diophantine equation of order in by "H.M" table:
Ÿ A new and fast method for calculating
"
" determinant (H.M method)
Ÿ Definition of regular and irregular prime numbers by "H.M" determinant
Ÿ New method of calculation of sum of
"k-th" power of the first "n" natural numbers by
"H.M" determinant (expressing "
" via a
determinant)
Ÿ Determining the number of roots of perfect cubic degree of equation directly by "H.M" method
Ÿ Proof of a new and applied "H.M" theorem (concerning the factorization of composite numbers)
21.1. Solving congruence and Diophantine equations
by "H.M" table (new method)
(1)
We call number "n" as module, "x" as unknown, "a" as coefficient of unknown and "c" as constant number of congruence.
We know that if "
" and
according to multiplicative inverse of "a" namely 
(multiplicative
inverse of "a" in congruence):
Equation (1) can be written in below form:
Therefore, for solving equation (1), it is enough to calculate inverse of "a". We know that inverse of "a", (multiplicative inverse of "a") is calculated from below congruence equation:
(2)
In equation (2) if 
and 
is
dividing residue of
, we can write:
(3)
Congruence equation (3) can be written in below Diophantine equation form:
(4)
According to "
" and if 
is
dividing residue of 
, we can write:
(5)
As previous stage, congruence equation (5) can be written in below form:
(6)
As the same method, If we continue this action, coefficient of unknown will be "1" and with return to previous stages, we can calculate "x" with a reversible method.
21.1.1. Attention.
We calculate all of above calculations with "4- row" table. This table has "4" rows that is completed after "4" stages.
For example we solve below congruence equation:
By using "H.M" table:
|
|
1378 |
621 |
136 |
77 |
59 |
18 |
|
|
2 |
1 |
|
|
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
|
|
|
621 |
136 |
77 |
59 |
18 |
5 |
3 |
2 |
1 |
|
|
|
537 |
242 |
53 |
30 |
23 |
7 |
2 |
1 |
1 |
|
5
3
21.1.2. Attention
Every table column, determines a congruence equation.
In this example, since
, so we must
calculate residue of dividing and write it in second mesh
of first row (from the left side) beside the module
.
Before explaining the table, we remind this point that for solving
every congruence equation, at first it is necessary to examine the condition
.
In congruence equation
, if
, so equation
has answer when "c" is divisible by
.
Therefore, for examining the condition, at
first always we calculate successive division in below form and write the
obtained residue in first row of the table respectively. If the first row of
the table is ended to number "1", it shows that condition is
established and if it is ended to zero and number before zero is greater than
"1", that number is the greatest common divisor of "a"
and "n".
Stage (1). We calculate successive divisions in below form and write obtained residues in first row of the table.
|
1999 |
1378 |
|
1378 |
621 |
|
|
1378 |
1 |
|
1242 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
621 |
136 |
|
3 |
2 |
|
|
544 |
4 |
, … , |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Stage (2). We write congruency’s constant number that
is "1" and "–1" successively in the second row of the table
(row
) from left to right.
Stage (3). We write the first residue (621) to the
last residue (1) another time in the third row (row
)
like the first row (ni).
Stage (4). Always we suppose the last mesh of forth
row in right side of table (row
) is equal to constant number (+1
or –1) of its column in second row. It is necessary to explain that in first
row, with condition, the number "1"
appears and so, division is finished.
For completing the forth row (row) of
the right side in successive "M" figures (according to figure
and in direction of arrows)
We
act in this method (action of every row, is written at beginning of every row):
We multiply the last number from the right side in forth row (537) in congruence constant number:
In the other hand, obtained residue of dividing number "537(1357)" or "728709" by "1378" is answer of congruence equation:
(Main answer of equation) 
It is obvious that general answer of equation for arbitrary
integer value of 
is:
(General answer of equation) 
21.1.3. Example
Solve below congruence equation:
Solution. Since "
", at
first we write obtained residue from division 
in the right
side of "module 19". Then we calculate successive divisions and write
obtained residues on first row of the table:
According to the above congruence, positive main answer of equation is:
; 
|
|
19 |
7 |
5 |
2 |
1 |
|
|
1 |
-1 |
1 |
-1 |
|
|
|
7 |
5 |
2 |
1 |
|
|
|
|
-3 |
-2 |
-1 |
|
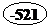21.1.4. Example
Find inverse of number "1999" with "module 1980".
Solution. Mathematics expression of problem is below congruence equation:
Since
, we write residue of division 
in
the right side of "module 1980" and then we calculate successive
divisions.
21.1.5. Attention
Since always our purpose is positive answer of equation, therefore, it is enough to add number of module (1980) to number (-521) that the main answer of equation is obtained:
|
|
1980 |
19 |
4 |
3 |
1 |
|
|
1 |
-1 |
1 |
-1 |
|
|
|
19 |
4 |
3 |
1 |
|
|
|
|
-5 |
-2 |
-1 |
|
So, multiplicative inverse of number "1999" in "module 1980" is "1459".
21.1.6. Example
Verify below congruence equation about existing or non- existing
answer: 
Solution. At first, we obtain the greatest common divisor of two numbers "3953" and "2680" with successive divisors and writing the residues.
|
|
3953 |
2680 |
1273 |
134 |
|
0 |
|
|
1 |
-1 |
1 |
-1 |
1 |
|
According to the table:
Since constant number of equation (176) isn’t divisible by "67", so equation hasn’t answer.
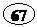21.1.7.
Example
Solve below congruence equation:
Solution. We solve the equation by forming the table:
(
)
|
|
77 |
69 |
8 |
5 |
3 |
2 |
1 |
|
|
1 |
-1 |
1 |
-1 |
1 |
-1 |
|
|
|
69 |
8 |
5 |
3 |
2 |
1 |
|
|
|
-29 |
-26 |
-3 |
-2 |
-1 |
-1 |
|
One answer of equation from infinite answers is:
Since we want positive answer of equation, therefore, we add
positive coefficient of module to this answer:
|
;
21.1.8. Example
Find inverse (multiplicative inverse) of number "34" with module "41".
Solution. This problem is equivalent with below congruence:
We solve the equation by forming table:
|
|
41 |
34 |
7 |
6 |
1 |
|
|
1 |
-1 |
1 |
-1 |
|
|
|
34 |
7 |
6 |
1 |
|
|
|
|
-5 |
-1 |
-1 |
|
According
to the table, answer "
" will be obtained that for
finding positive answer; it is enough to add the module to it:
|
;
Therefore, inverse of number "34" is number "35" with module "41".
21.1.9. Problems
Ÿ By using the table "H.M", solve below congruence equations.
|
1) |
, |
2) |
|
3) |
, |
4)
|
|
5) |
, |
6) |
|
7) |
, |
8) |
(
:
answer)
(
: answer)
21.1.10. Attention
This table has a lot of usage’s that we explain the usage of table in solving linear Diophantine equations briefly. This table can be used for identifying the prime numbers and finding equivalent of exponential numbers etc.
21.2. Solving linear Diophantine equations by "H.M" table
We consider two-unknown Diophantine equation in below general form:
(1)
We write equation (1) in below congruence equation form:
(2)
Now, we solve equation (2) by table and determine value of
.
Then we obtain value of 
from relation
.
21.2.1. Example
Solve below Diophantine equation.
(1)
Solution. At first, we write the equation in below congruence equation form:
(2)
Now, we solve congruence equation (2) by the table:
|
|
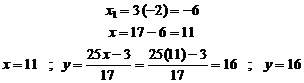
17 |
8 |
1 |
|
|
1 |
-1 |
|
|
|
8 |
1 |
|
|
|
|
-1 |
|
21.2.2. Attention
If we have a special answer of equation (1), we can write general answer of
equation, because if 
is a special
answer of equation, then:
If
, by subtracting the two
equations of system:
In order to
, it is necessary to have:
Therefore, if
, answers of equation (1) will be
obtained from below equations:
According to equations (3), general answer of equation 
is:
21.2.3. Example
Solve below Diophantine equation.
Solution. At first, we write equation in below congruence equation form:
(1)
Now, we must obtain product of (1340, 3953):
|
|
3953 |
1340 |
1273 |
|
0 |
|
|
1 |
-1 |
1 |
-1 |
|
Since the first row is ended to "Zero", it is results that numbers "1340" and "3953" have common factor "67":
In the
other hand since
, therefore we can simplify
equation (1) to 67: 
Here, for solving equation (2), we form the table:
|
|
59 |
20 |
19 |
1 |
|
|
1 |
-1 |
1 |
|
|
|
20 |
19 |
1 |
|
|
|
|
1 |
1 |
|
According
to the table:
If we have value of, we can
calculate value of:
Therefore, the general answer of equation is:
21.2.4. Example
Obtain positive and integer answers of below Diophantine equation:
(1)
Solution. The greatest unknown coefficient is
coefficient of
, therefore:
So, we can write:
(2)
With forming the table:
|
|
11 |
7 |
4 |
3 |
1 |
|
|
1 |
-1 |
1 |
-1 |
|
|
|
7 |
4 |
3 |
1 |
|
|
|
|
-2 |
-1 |
-1 |
|
According to below congruence:
Values of 
and 
are:
As the same method:
(3)
In this congruence equation, coefficient of unknown 
is
"7" and the module is 
according to congruence
(2). Therefore, answer of equation (3) according to the recent table is:
Equation (1) hasn’t integer answer for 
and
,
so equation has two kinds of special answers 
and 
that
we can obtain general answers of equation by using these special answers.
21.2.5. Problems using the table "H.M" solve below Diophantine equations
1) If
, find integer numbers 
and
so that below equation is
established.
2) 
3) 
4) 
5) 
21.3. Solving "n-th" degree Diophantine equation by "H.M" table
We consider below "n-th" degree Diophantine
equation, we determine positive values of and for
it:
(1)
For solving equation (1), we write it in below congruence equation form:
(2)
It is obvious that condition of existing answer for equation
(2) or (1) is that
, so, equation (2) or (1) has
"m" two by two non-congruent answers (different answers) with
module
.
In the other hand, if
, we write
equation (1) in below form:
(3)
By using the table (H.M), we solve equations (2) or (3).
By using the table (H.M), answers 
or
will be obtained for (2) and (3)
respectively therefore, if
, we gain these answers:
(I) , 
(II)
Here, If value of exists,
it is resulted from relation (II):
(4)
If we consider 
and 
limits of
will be determined:
(5)
Positive and integer values of 
are
determined according to (5) and relation (II).
For example, we solve below fifth degree equation and we find its positive answers:
(1)
At first, we write equation (1) in below congruence equation form:
(2)
We simplify equation (2) and then solve it by table (H.M):
(3)
According to the table (H.M):
|
|
29 |
4 |
1 |
|
|
1 |
-1 |
|
|
|
4 |
1 |
|
|
|
|
-1 |
|
|
Therefore, answers of equation (3) are:
(4)
By substituting the values of in
(1):
(5)
According to "
"
and "
", Suitable value of is
determined from equation (5):
Here, by substituting 
in
equation (4), will be obtained:
For another example, we solve below equation and obtain its positive answers:
Since we want positive answers of equation, therefore, we
determine limits of and .
If "
" ; then 
or
that it is enough to test
the
main equation only for five primitive natural numbers:
Therefore, an answer of equation is "
"
and "
".
Substituting another four natural numbers instead of (in
main equation), no other positive answer will be obtained.
21.3.1. Remark
If "
" and "",
then equation (1) is solvable easily, because, we can calculate limits of and
in this case, it means that
we write equation (1) in "
" or "
"
form ("
"and "y" are
positive):
21.3.2. Example
We solve below equation:
Since we want positive answers of above equation, we can
calculate limits of and from
the main equation:
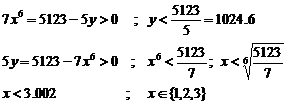
By substituting three numbers that have been obtained for,
value of 
and then 
will
be obtained. Therefore, we have determined the only positive answer of equation
by limits check method. In this method, it is enough to determine the limits of:
21.3.3. Remark
If 
be a prime number, equation
(1) changes to below easy and solvable form:
(6)
We write equation (6) by using the Fermat’s (smaller)
theorem 
in below form:
(7)
Answer of equation (7) can be calculated by using the table (H.M) easily.
21.3.4. Example
We solve below 7-th degree Diophantine equation:
(1)
Solution. According to
, we divide
equation (1) by "2":
(2)
We write equation (2) in below congruence equation form:
(3)
According to Fermat’s (smaller) theorem 
equation
(3) changes to below equation:
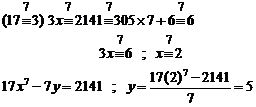
Therefore, answers of equation (1) are in below form:
Here, it is enough to calculate value of with
respect to:
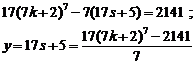
Answers of equation:
|
k |
0 |
1 |
2 |
… |
|
x |
2 |
9 |
16 |
… |
|
y |
5 |
683263 |
651914373 |
… |
21.4. A new and fast method for calculating of "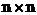
"
determinant
("H.M" method)
For showing new method of calculation of determinant, it is enough to calculate some determinant in general and numeral cases. Therefore, we calculate third and forth order determinant in general and numeral case.
21.4.1 Calculation of third order determinant
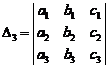
Calculation method. According to the determinant
rules always we can suppose that medium element of first column namely 
is
non-zero
. Therefore, we reduce 
with
chain second order determinant method.
Action method. At first, we write second row another
time. In next stage, we put the obtained first column between second and third
column another time. Then we separate the obtained element to
"four-classes" in a 
determinant that we have a determinant
so that one of its elements is a determinant itself. At
last, for calculation of, it is enough to divide the
obtained value by.
Action stages. We write the second row another time and we put obtained first column between second and third column another time. Then separate the obtained element to "four-classes":
Stage 1:
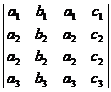
Stage 2:
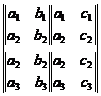
Every one of
"four-classes" forms a determinant. Then by
calculation of every one of determinants and general
determinant and dividing obtained number by, value of will
be calculated.
Stage 3:
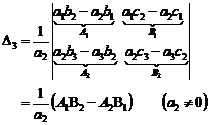
Therefore is:
After necessary abridgment:
21.4.2. Example
Calculate below determinant:
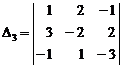
ŸCalculation with second order chain determinant method
1) We write the second row another time:
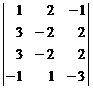
2) We write obtained first column another time:
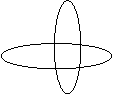
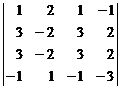
3) We have separated to second order determinants:
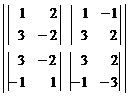
4) We calculate the second order chain determinant:
5) We divide the second order chain determinant product by middle element of determinant’s first column:
6) Calculated value of
:
21.4.3. Simplified method of chain determinant
Here, we present simplified and brief method of second order chain determinant. At first, we separate first column and perform actions on successive rows
in below form:
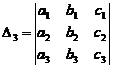
(According to the determinants rule, we suppose that "
")
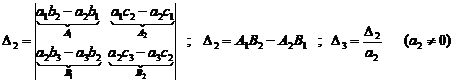
Here, we calculate example (1) (chain determinant of second order) by simplified method.
At first we separate the first column and perform actions on
rows and then we calculate "
".
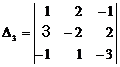
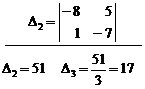
2) Calculation of forth order determinant in separation method (chain second order determinant):
With the same method, at first we reduce 
to
and then reduce to
chain second order determinant like before.
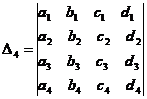
For separation "
" to
second order determinants, it is enough to write second and third rows another
time and write obtained first column alternately repeatedly and then we perform
the separation. Here, according to determinants rules, we suppose 
,
(like with changing two
rows or two columns). Therefore, always we can suppose that ",",
then with this hypothesis:
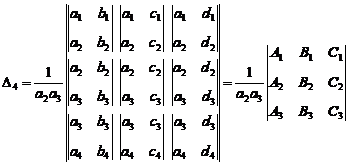
According to the determinant rules, we can suppose that
"
" and so:
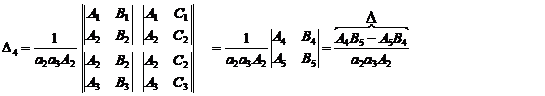
Now, we present simplified method of chain second order determinant:
At first we separate first column and then we perform the
actions on rows in below form (we suppose
):
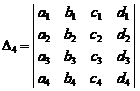
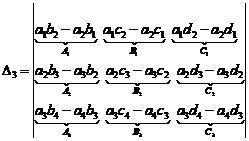
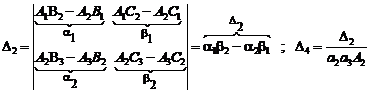(Final result)
21.4.4. Explain
It is necessary to explain that for calculation of the
"n-th" order determinant when
, simplified
method of chain second order determinant can be used also, because for higher
order of determinant, we need a method with higher speed. For calculation
,
we must attend that first column middle elements of every stage, namely
,
,
and … must be non-zero. For
example for calculation 
, we must have 
;
because in stage(1) of , we must have 
,
and in stage (2) of 
, we must have 
and
in stage (3) of , we must have 
.
It is clear that according to determinants rules for every stage, this thesis
is certain and it hasn’t any disorder to generality of problem.
21.3.5. Example
Calculate "forth order" determinant by chain
second order determinant method.
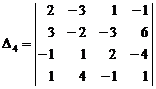
Calculation with chain second order determinant method:
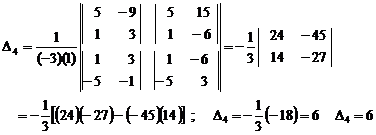
Here, we calculate example (21.4.5) by simplified method of chain second order determinant.
In order to this, at first, we separate the first column and perform the calculation on rows in below form (like third order determinant):
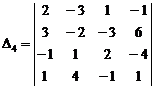
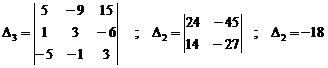
21.4.6. Example
Calculate below "fifth order" determinant.
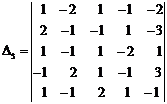
Solution. We perform calculation on rows and then we
obtain, 
and 
determinant.
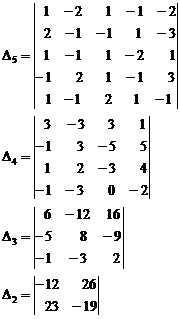
Product of determinant is:
21.5. Definition of regular and irregular prime numbers by "H.M" determinant
Below Congruence is result of theories related to verification of Fermat’s last
theorem:
Here, Congruence 
is equivalent
with congruence
and below theorems are resulted
from congruence (1).
21.5.1. Theorem
Number 
is irregular if and only if
a number exists for 
so that 
is
divisible by
.
21.5.2. Theorem
Number 
is regular if and only if
for every
, number
isn’t divisible by.
It is easier to consider the general sum:
It can be proved easily with mathematic induction that
numbers
, values of polynomial 
of
degree for 
that
has rational coefficients (
: Bernolli’s numbers):
It is interesting that Bernolli’s numbers entered into mathematics during solving one of astronomy problems.
The subject is that infinite sequence of Bernolli’s numbers appears during converting some simple functions as power series. Like, we can prove:
This series was put against Bernolli during astronomy examinations.
This point that in series related to extension of 
,
only Bernolli’s numbers appear that have an even index, isn’t randomly, because
we can prove easily that all of Bernolli’s numbers that have odd index (except
number 
), are equal to "zero":
If 
then 
Bernolli’s numbers with even index
,
have interesting characteristics. Like values of famous "Riemann's
function" (function
), can be expressed with respect
to Bernolli’s numbers when have even power:
The first Bernolli’s numbers are in this form.
The numerators of these fraction increase rapidly, For example:
Suppose:
is indicator of number
. Without
special difficulty we can prove that for
, denominator 
from
number 
isn’t divisible by.
But, for every
, we have this equality:
It means:
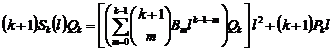
Therefore, for
, the number in right side of
parenthesis is an integer number.
We return to previous congruence (module
) and
we simplify it to
, so, the result is:
Therefore, congruence "
" is
established if and only if we have:
Therefore, we can present Kummer's theorem.
21.5.3. Kummer’s theorem
Prime number is regular if and only if it is
not a divisor of numerators of Bernolli’s numbers in "
"
form.
We express some examples (see the Bernolli’s numbers that we expressed before):
isn’t divisible by "5".
and 
aren’t
divisible by "7".
and 
aren’t
divisible by "11".
and 
aren’t
divisible by "13".
and 
aren’t
divisible by "17".
and 
aren’t
divisible by "19".
and 
aren’t
divisible by "23".
Therefore, all of these powers are regular.
In other word, Fermat’s last theorem is correct for powers "5,7,11,13,17,19 and 23".
21.4.4. Attention
In next section, you will be acquainted with "H.M"
new method of calculation of 
that is expressed by a
determinant.
We present calculation 
by
determinant without proof ("H.M"
method):
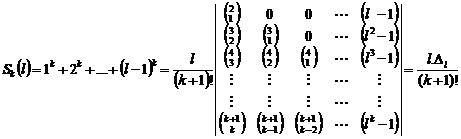
21.5.5. Result
Since 
is a prime number and
,
so
.
Number is a regular prim number if and
only if 
is not divisible by for
every
.
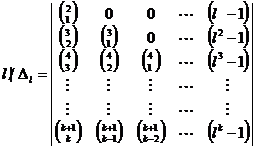
In fact, according to identification function of prime numbers, we can write:
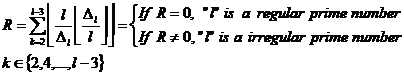
Therefore, set of regular prime numbers is defined in below form:
(Set of regular prime numbers)
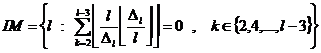
It is obvious that according to definition of set of regular prime numbers, set of irregular prime numbers can be defined by definition of prime numbers set:
(
: Set of irregular prime numbers)
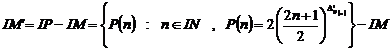
Here, sets of regular and irregular prime numbers are
defined by expressing "
" and definition of prime
numbers set "IP".
Calculation of "
".
New method for calculating the sum of "k-th" power of 
natural
numbers 
by determinant
Here, we prove that "
"
calculates by below "k-th" order determinant:
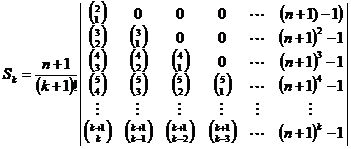
21.5.8. Result
Fermat’s last theorem is correct for powers
.
21.5.9. Important result
Other sets can be defined by prime numbers formula.
Here, sets of regular and irregular prime numbers are
defined by expressing and definition of prime
numbers set "
".
21.6. New method of calculation of sum of "k-th" power of the
first "n" natural numbers by "H.M"
determinant
(expressing "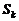
" by a determinant)
Here, we prove that "
" can be
calculated by below "k-th" order determinant:
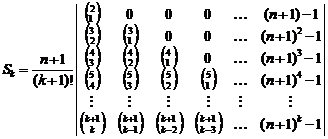
Proof: We know that if 
then:
We put
,
and 
in
above identity:
Now, if we put values 
respectively
in above identity, we have below equality with adding obtained relations:
We write above equality in below form:
Now, if we put values 
respectively
for, below system will be obtained
:
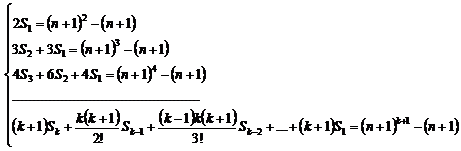
So:
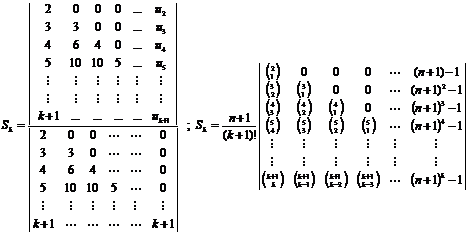
21.7. Determining the number of roots of perfect cubic degree equation directly by "H.M" method
(1)
In equation (1), if we have:
then equation has a real root that is computable easily,
therefore for calculating the root of equation (1) it is enough to perform this
conversion 
and establish the above
mentioned conditions. As we know, after conversion we will have below equation:
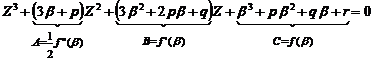(2)
Now, for calculating
, we establish
the first condition namely
. After establishing this
condition we will see that value of is not
obtained.
Now, we establish the second condition, namely
.
And we will see that value of will be calculated.
Therefore:
(3)
After summarizing relation (3), we have below second degree
equation (with respect to):
(4)
Here, for calculating the value of, it
is enough to solve the second degree equation (4). After solving equation (4),
the value of is:
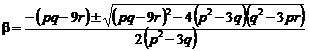(5)
Discriminant 
of cubic degree equation
(1) is obtained from value of:
(6)
Here, with obtaining such equation, we can discuss about the number of its roots:
1) If
, then equation (1) has a real
root and two complex roots.
2) If
, then equation (1) has an
additive root and one simple root.
3) If
, then equation (1) has three
real roots.
21.7.1. Remark
In equation (1), If
, then the
equation is:
(7)
It means the focal equation of cubic degree will obtained.
Now, if we put value 
in Discriminant of
equation (1), Discriminant of focal equation (7) will
obtained:
21.8. Proof of a new and applied "H.M" theorem
(Concerning the factorization of composite numbers)
21.8.1. "H.M" Theorem
If 
is divisible by "p"
and result of 
is an odd number, then:
Proof. For every and 
,
we can write:
(1)
If 
is odd and according to
below equality for every odd
:
(
: Number integer part)
(
is odd
number) 
So:
(2)
21.8.2. Example
If 
is prime number, according
to Wilson’s theorem, expression 
is divisible by and
conversely (If 
is divisible by and
is a prime number).
Therefore, if 
is factorization in
relation (2) form, is a prime number:
(3)
21.8.3. Example
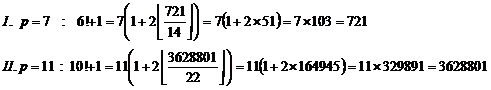21.8.4. Example
I. If 
then:
(p: prime number)
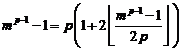
II. If 
then: