CHAPTER 22
The abstract of formulas and their software programs
Appendixes (II)
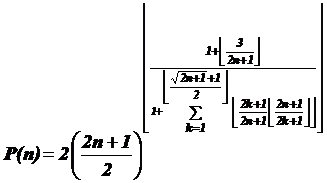
(Domain function)
(Natural numbers set)
(Range function) 
(Prime numbers set)
Contents:
Ÿ The Abstract of the formula of the
prime numbers generator
Ÿ The Program of the prime numbers
generator
Ÿ The program for distinction of the prime
numbers
Ÿ The abstract of the formula of the
determining of the "k-th" prime number
Ÿ The Program for determining of prime
number "k-th"
Ÿ The Abstract of Riemann’s Zeta
equation solution
Ÿ The Program for determining of the
number of the prime numbers smaller than or equal any arbitrary number "p"
exactly
Ÿ The abstract of the definition of the prime numbers set by using the surjective generating function of the prime numbers (IP).
Ÿ The program for the definition of the
prime numbers set
.
Ÿ The abstract of the definition of the Mersenne’s prime
numbers set by using the prime numbers generator
.
Ÿ The program for the determining of the Mersenne’s prime numbers of M-digits by using prime numbers formula (M: Arbitrary number).
Ÿ The New Mersenne’s prime number as "42nd" known Mersenne prime found (February 2005).
Ÿ Determining of generating function of the prime numbers greater than the greatest prime number (by prime numbers formula)
Ÿ Determining of generating function of the prime numbers greater than the greatest prime number (by prime numbers formula)
22.1. The abstract of the distinction formula
of the prime numbers
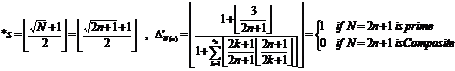
For Example 1:
|
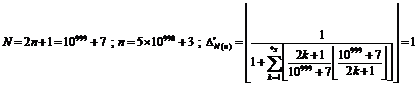
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
... |
|
... |
|
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
... |
|
... |
|
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
... |
1 |
... |
22.1.1. Testing the program[1] o f"
" for
distinction of "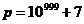
"
22.2. The distinction program of the prime numbers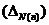
This program"
" is for testing the formula
.The purpose
of this program is distinction of prime numbers. With running this program when
the program require to enter a number, then enter a number, and press the enter
key, so the program will tell you that this number is prime or not.
22.3. The abstract of the formula of the prime numbers generator
22.3.1. Example
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
... |
|
|
3 |
5 |
7 |
p |
11 |
13 |
p |
17 |
19 |
p |
23 |
p |
p |
29 |
31 |
... |
22.4. The final formula of the prime numbers generator
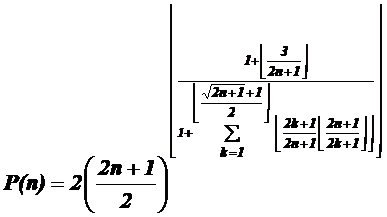
(Domain function) 
(Natural numbers set)
(Range function) 
(Prime numbers set)
22.4.1. The definition of the prime numbers set by onto generating function
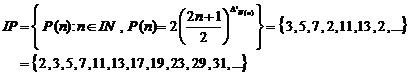
22.4.2. The running of Euler’s special prime numbers formula[2]:
22.5. The program [3]
of the prime numbers generator (
)
22.5.1. Example
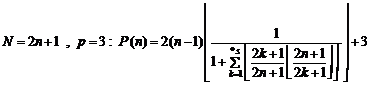
22.5.2. Program"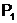
":
This program is for testing the relation 
the purpose
of this program is generating of prime numbers. After running this program at
first the below message will appear:
"Enter Down Limit"
and then message
"Enter Up Limit"
In answer to this message we should enter the down limit and
up limit of natural-subset that we want to enter the numbers of "1"
up to "1000,000" after pressing the enter key. All of the prime
numbers between "1" and "1000, 000" will be saved as a file
to the name of 
[4]
22.6. The abstract of the formula of the determining of
the "k-th" prime number (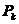
):
22.6.1.
22.6.1.1. Example:
|
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
... |
|
k |
2 |
3 |
4 |
5 |
5 |
6 |
7 |
7 |
8 |
9 |
9 |
... |
|
|
3 |
5 |
7 |
0 |
11 |
13 |
0 |
17 |
19 |
0 |
23 |
... |
22.6.2.
22.6.2.1. Example:
|
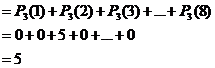
k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
... |
|
|
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
... |
22.7. A program for determining the prime number "k-th" ()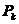
This program "
"is for testing the formula
""
from part (22.6.1). The purpose of this program is calculating the prime number
"k-th".
22.8. The abstract of Riemann's zeta equation solution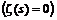 
22.8.1. Riemann's Zeta Function
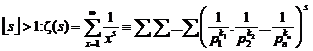
22.8.2. Riemann's Zeta
equation"
"
22.8.3.
The determining of the number of the prime numbers less
than or equal any arbitrary number "p" exactly
:
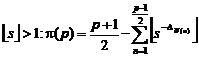
22.8.4. Example
|
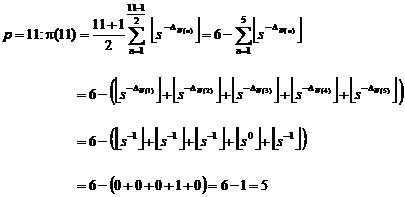
P |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
... |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
... |
22.9. A program for determining of the number of the prime numbers smaller
than or equal any arbitrary number "p" exactly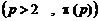 
This program (
) is for testing part (22.8.3).
The purpose of this program is determining the number of the
prime numbers before
. For example, if you enter a
prime number like, the program will give you
number "6" in answer that shows number is 
prime number.
22.10. The abstract of the definition of the prime numbers set by using the
surjective generating function of the prime numbers (
)
22.10.1. Example
|
P=2: |
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
... |
|
|
3 |
5 |
7 |
2 |
11 |
13 |
2 |
17 |
19 |
2 |
23 |
2 |
2 |
29 |
31 |
2 |
2 |
... |
22.11. A program for defining the prime numbers set ()
This program (
) is for testing (22.10). The
purpose of this program is determining the prime number set. In below form:
22.12. The abstract of the definition of the Mersenne's prime numbers set
by using the prime numbers generator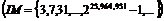 
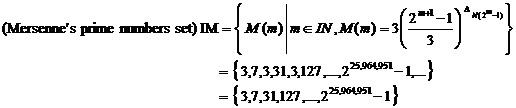
22.12.1. Example
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
... |
|
|
M(m) |
3 |
7 |
3 |
31 |
3 |
127 |
... |
|
22.13. A Program[5] for determining the Mersenne’s prime numbers of M-digits (M: Arbitrary number)
Note. This program designed for determining of the
power of new Mersenne’s prime number (Power "p" in 
by using of
previous Mersenne’s prime numbers power). Here, look at the part of program and
running its results. It dose contain "25" pages and about
"500" lines.
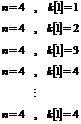
The Result is: 25, 964, 951
22.13.1. Notice
If in procedure of running, for titan numbers you faced with a problem, this problem is not related to the programming. The used variables in program although selected with long length. They have so limitation. For huge and complicated calculations, we must used from variables with longer length (if exist) and for the most complicated calculations we should used super computer.
22.14. The new Mersenne’s prime number as "42nd" known Mersenne prime found (February 2005)
On February 18, 2005, Dr. Martin Nowak from Germany, found
the new largest known prime number,
. The prime number has 7,816,230
digits! It took more than 50 days of calculations on Dr. Nowak's 2.4 GHz
Pentium 4 computer. The new prime was independently verified in 5 days by Tony
Reix of Grenoble, France using a 16 Itanium CPU Bull NovaScale 5000 HPC running
the Glucas program by Guillermo Ballester Valor of Granada, Spain. A second
verification was completed by Jeff Gilchrist of Elytra Enterprises Inc. In Ottawa,
Canada using 15 days of time on 12 CPUs of a Compaq Alpha GS160 1.2 GHz CPU
server at SHARCNET.
Dr. Martin Nowak, an eye surgeon in Michelfeld, Germany learned of GIMPS in April 1999 when he red an article his newspaper, the "Frankfurter Allgemeine Zeitung". Dr. Nowak, a math hobbyist, started with one PC and as his practice grew so did his participation in GIMPS. Six years later, he has 24 computers doing calculations for GIMPS—and one Mersenne Prime to his credit!
Perfectly Scientific, Dr. Crandall's company which developed the FFT algorithm used by GIMPS, makes a poster you can order containing the entire number. It is kind of pricey because accurately printing an over-sized poster in 1-point font is not easy! Makes a cool present for the serious math nut in your family.
Dr. Nowak could not have made this discovery alone. In recognition of contributions made by tens of thousands GIMPS volunteers, credit for this new discovery will go to "Nowak, Woltman, Kurowski, et al". The discovery is the eighth record prime for the GIMPS project. Join now and you could find the next record-breaking prime! You could even win some cash.
For more information on this latest prime discovery read the full press release[6]
22.15. The determining of generating function of the prime numbers greater than the greatest prime number (by prime numbers formula)
For determining the generating function of an unknown large
enough prime number on other word the generating function of the numbers
greater than the greatest prime number which is the "42nd" known
Mersenne prime namely "
" is defined as follows:
(1)
Therefore, the following functions produce either
, which is the
greatest known prime number or the prime numbers after this number:
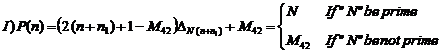
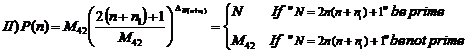
The function in (1) is introduced as the generating function of the unknown large enough prime numbers.
In order to find a prime number large enough by using a computer, there are a lot of algorithms. Each of these algorithms because of its digital inherence is not able to distinguish the prime numbers after a specific large number. So, we should define a function which is able to produce the numbers greater than the greatest known prime number. The following function is a kind of these functions:
(2)
