CHAPTER 4 of The discovery of prime numbers formula and its results

CHAPTER 4

On the history of the problem of recognizing prime numbers by two sided theorem in particular Wilson’s theorem and its consequences

4.1. Wilson’s theorem

In order to a non-one natural number "m>1" be prime, the necessary and sufficient condition is that "m" aliquot (m-1)

Proof. At first, we prove theorem inverse. We suppose that

(1)

If "m" is not prime number, a natural number like "d" is one of numbers. d| (m-1)! . In other words, according to the thesis . So, according to (1), it is impossible. Now, we conclude Wilson’s theorem from Dirichlet’s theorem.

4.1.1. Lemma

Suppose that "p" is odd prime number and. If a number like "b" exists so that then, congruence has two non- congruent answers whit module "p" exactly.

Proof. At least two non- congruent answers exists for congruence. Because:

For we show that congruence hasn’t another answers except these two answers. For this purpose suppose that. Therefore . So then or . In first case is and in second case is:

4.1.2. Dirichlet’s theorem (1828)

Suppose that "" be prime number and If congruence hasn’t answered, then and if has answer.

Proof. If "", then assertion is obvious. So suppose "" is prime number. According to theorem, if , then there will be an individual number "n", so that 1 and . Now, we call number "m" and "n" as corresponding. If hasn’t answer, then for corresponding numbers "m" and "n" we will have . Therefore, we can classify the integer numbers in the interval "1" up to to couples of corresponding numbers. Multiplication of all these corresponding numbers is congruent with to module "p" and obviously it is also congruent with. Therefore . If the congruence is solvable so there is an answer like "b" that "".

Another answer of this congruence is. Now we consider as residual number. It is obvious that these number, aren’t answers for congruence. Therefore we can convert them to corresponding pairs.

Multiplication of these pairs is congruent to module "p" with and, so:

We see that grand result of Dirichlet's theorem is Wilson’s theorem. In 1771, Lagrange presented a very complicated proof of Wilson’s theorem. But Wilson’s theorem is obtained simply from theorem (4.1.2).

4.1.3. Wilson’s theorem

If "p" be prime number, then ""

Proof. In (4.1.2) theorem we set, especially has answer. So:

Therefore, Wilson’s theorem is a test for primality of considered number.

Although this test is unusable, because is a very big number.

4.1.4 Euler's test

Consider that "p" be prime and. So congruence is (is not) solvable

if:

Proof. Consider that congruence has answer. Therefore, according to Wilson’s theorem:

;

Now, factorize result is obtained by multiplication of both side in "–1". If congruence hasn’t answer, proof it the same.

4.2. Remarks concerning Wilson’s theorem and
its converse and corollaries

I. First time, Werring in his book "thoughts in algebra" (1770) concerned theorem to sir john Wilson (1741-1793), so this theorem is known as Wilson’s theorem Although Leibniz had said an equivalent assertion. The inverse of theorem was propounded by Lagrange (1771) who also proved.

II. Wilson's theorem gives a simple criterion for investigation the investigating the primality of non-one natural number "m". It is enough to identify that is divisible by "m" or not. But this criterion has no practical advantage. Because in crease with "m", rapidly.

III. According to Wilson's theorem, for each prime number "p" number is a natural number. Every prime number like "p" so that is a natural number, has called as a Wilson’s prime number. By testing, it’s clear that only 5, 13, 563 are Wilson’s prime numbers among prime numbers:

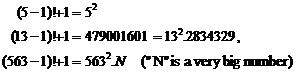
4.3. Corollaries of Wilson’s theorem

4.3.1. Example 1

If "p" is a prime number and , then:

Proof. Congruence (1) is established for by Wilson’s theorem and it is provocations for p=2.

We suppose that and congruent are in module "p". Since, so:

According to and Wilson’s theorem:

4.3.2. Benefit

Suppose that "p" is an odd prime number. Order (1) in last example results for :

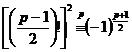(2)

So, if "p" be or then:

() (3)

() (4)

For example:

()

4.3.3. Example

If and only if odd prime number "p" to be in form of "" then.

4.3.4. Example

The number of natural numbers like "n" that is composite for them is infinite.

4.3.5 Example

If and , then "m" is composite. Conversely, if "m" is composite and distinguished from 4, it adapts in (*).

4.3.6. Liouville’s theorem

If be prime number and greater than "5", for every natural number of :

(5)

4.3.7. Leibniz’s theorem

The condition of necessary and sufficient in order that natural number of be prime:

(6)

4.3.8. Remark

If multiply expression of in the two side relation (6), then to obtain Wilson's theorem:

; (7)

Here, we present some determinate function formula by Wilson's theorem:

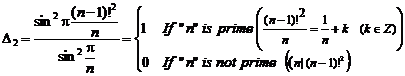
4.3.9 Remark

According to Wilson’s theorem, supposing that "k" is an integer number, for every and :

(5)

It is necessary to mention that we can build a lot of identification functions by using the Wilson’s theorem, that for example, we present one of them:

[1] (6)

(: Number integer part)

4.3.10. Explanation

By Wilson’s theorem even can not testing number "100001" limit of defines in below form:

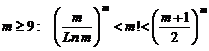(11)

Of course, we sow important results of this theorem. Very mathematicians presented a lot of theorems and testing for characteristic of prime numbers that we will attempt which showing on the history of obtained results.

Here, with present other formula for characteristic of numbers that very interesting and it express by Euler’s arithmetic function namely we follow subject:

We can determine number by below determinant:

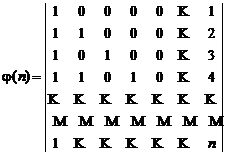
4.3.11. Explanation

In these functions number ofexist. It is obvious that working with it is impossible and even for a number near to, it is also unfaultable. For this reason, these identification functions can’t be useful in real and in fact we can use them to present pure theories, because for example the number" 69!" is greater than (a 99 digits number).

4.4. Some of if theorems for recognizing prime numbers

4.4.1. Lemma

The congruence is establish for every prime value of "n" and no natural composite number adapts in that , except of 4, 6, and 22.

4.4.2. Subbarao`s Theorem (1974)

If, then "n" is a prime number, if and only if :

4.4.3 Lemma

If "p" is a prime number then for every natural number "n":

4.4.4. Theorem

If and only if natural number to be prime number then for every natural number "n", so that :

4.4.5. Theorem

If and only if natural number to be prime number then for every natural number "n":

4.4.6. Introduction to Mann and shanks criterion for primality

At first we express this interesting criterion with language which its discoverers said and then by mathematics language as a theorem.

In Pascal mathematical triangle, we transfer every row two cell toward right, so that the coefficients in "n" the row, namely the numbers:

Start from "2n" column and finish in "3n" column. Then mentioned triangle changes some part of it is shown below:

k n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
0	1
1			1	1
2					1	2	1
3							1	3	3	1
4									1	4	6	4	1
5											1	5	10	10	5	1
6													1	6	15	20	15	6	1
7															1	7	21	35	35	21	7	1
8																	1	8	28	56	70	56	28	8
9																			1	9	36	84	126	126
10																					1	10	45	120
11																							1	11

In this new table, in "n" row, entries which are divisible by "n", has been printed in bold letters. Like "1" and "1" in row "1" and "2" in row "2", "3" and "3" in row "3" and etc.

4.4.7. Theorem

If and only if the numbers of column "1" in above table to be prime then all coefficients this column, become printed in bold letters. According to the structure of the table, only and only an entry of "n" row is in "k" column that. In other word only and only an entry of "n" row is in a specific "k" column when .

4.4.8. Theorem (Mann and Shanks)

If and only if for every non-one natural number "k" to be prime number, then for every "n" ():

4.4.9. Theorem (Montferrier)

If "N" is odd and greater than 9 and if and only if "N" is prime number then below numbers:

aren’t perfect square.

Because, it is obvious:

4.4.10. Euler’s method

Some numbers are representable as sum of two perfect squires in two different ways. For example:

representations which their difference is just in arranging of factors aren’t distinct. We can factorization these numbers to multiplication of two factors. Fernekle and Mersenne discovered this thought but widely. Apparently we express solution of factorization problem we say some primary observation.

I. necessary condition for an odd number to be sum of two squares is that it be in "" form.

II. We consider that

(1)

If then repeating the above reasoning relation (1) will result a relation like and.

III. If equality (1) is established and but, then, so: .

4.4.11. Theorem

Every natural number is composite if it has two different representations of sum of two squares.

Also:

So:

4.4.12. Remark

The mentioned decomposition method in above theorem is Euler’s method. For using in decomposition of an odd number like "N", at first we must sure that this number is in the form of "". (For example:).