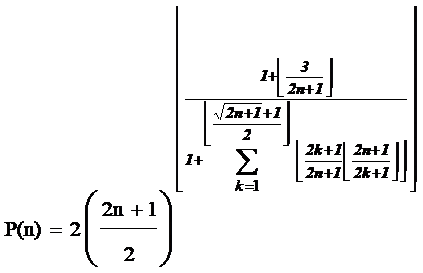CHAPTER 7
Decisive solution to the problem of finding the generator of prime numbers via discovering the surjective generating function of prime numbers
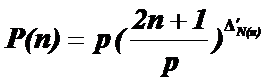
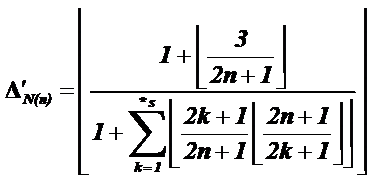
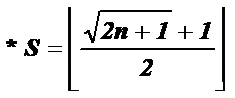
7.1. Determination of the formula for the surjective generating function of prime numbers
Here by using the identification function
, we can write onto
generator function of prime numbers.
For this purpose, at first we consider 
and "p"
is an arbitrary prime number. We know that "N" is prime or
composite.
It is enough to use identification functionfor definition
"N" in view of primality (be prime number or be composite):
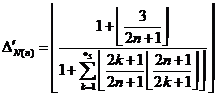
It is obvious that always have two cases,
"0" or "1". It means that if "N" be
composite,
is
"0" and if it is prime is "1".
Therefore, below function produces all of odd prime numbers
:
7.2. Domain and range of the surjective generating function of prime numbers
In fact Domain and Range of function "
" is:
(Domain)
, (Range)
Now by a transferring, it is possible to obtain the function "P" with below formula:
If "p" is considered as an arbitrary prime
number, according to function "" and translation of axes to 
Domain and range of new function "P" is:
Domain and Range of this function is:
and
Therefore, the function with below formula produces just prime numbers and in fact this range function is set of prime numbers:
Substituting, the formula of prime numbers or 
onto function
is:
According to primary condition, we form below table:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
… |
|
|
3 |
5 |
7 |
2 |
11 |
13 |
2 |
17 |
19 |
2 |
23 |
2 |
2 |
29 |
… |
Another function can be made equal with (*) function, for example:
; 
Domains and ranges of these functions are:
, 
Because:
Therefore, functions 
and 
also are equal to the function
"P". Here by using onto function "P"
(generator of all prime numbers) or functions and, set of prime numbers can be
defined below in forms:
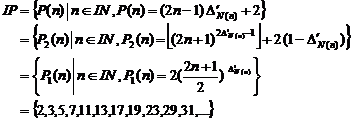
7.2.1. Result
If we consider "p" as an arbitrary prime number, then, formula of prime numbers can be considered in one of two below general cases:
7.2.2. "H.M" theorem
If 
and
then 
is prime and
:
