CHAPTER 8
On the history of the problem of determining the number of prime
and its related functions "
"and "
"
8.1. An introduction to the function "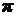
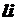"and "
"
"
" and "
"
functions which we will be acquainted with them are important functions that
are used in number theory. In these discussions, we prove some of primary
properties and say some information about it and we will be acquainted with
Chebyshev’s theorem about restriction "
".
8.1.1. Attention
After this, "x" is a real and positive
number and "
" means natural logarithm.
8.1.2. Definition
For every positive real number "x", "" is the
number of prime numbers which aren’t more than "x".
8.1.3. Direct results of definition
I. With definition, it is clear:
(1)
That "
" includes all of prime
numbers "p", then it adapt in 
propositional. Below relations
are some of direct results of definition:
(2)
(3)
(4)
(
is r-th term of prime numbers
sequence) Specially:
(5)
Generally if 
then 
then it is possible to show the
sequence of prime numbers not more than "x" as follow:
(6)
II. If "x" and "y" be two
real numbers and "
", then:
(7)
8.1.4. Remark
We can define "
" according to this formula
(7)for every x (positive or non-positive). However, because first prime
number is "2", for "
" we have "
".
III. "" function is ascending with
above assumption about "x" and "y":
(8)
We will acquaint with some of other primary properties of
"
"
function.
8.1.5. Theorem
For "
":
(9)
Now we start to restrict "" from bottom.
8.1.6. Theorem.
Always:
(10)
Proof. As usual, we consider that "e"
is bray centric logarithm
. If "
" then "
". Now we
consider that "
" and we select strictly
ascending sequence namely:
It is clear that there is a natural number like "n",
so that "
":
So:
Therefore, because "" function is ascending,
"
"
in the other side, because "
", according to logarithm
properties, "
" and
.
This inequality is very weak, and information about it is so
little. For example for "
":
So, information that is "
" although "
".
8.1.7. Theorem
Always:
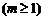(11)
Proof. According to previous theorem, we consider
that "
".
So prime numbers which aren’t more than "m", are:
Therefore, "
" and "
" and this
is equal to (11) inequality. According to (11) inequality, for example:
And this is also very little with respect to real value of
"
".
8.1.8. Theorem
For every natural number "n":
(12)
Proof. According to inequalities of theorem (8.1.7) ,"
" this
inequality is equal to (12) inequality.
8.1.9. Result
According to above theorems, always:
(13)
But don’t think that research problem about measure of
"
"
can be solved by these inequalities. In fact finding a good approximate value
for ""
is most complicated than it seems firstly.
According to above inequalities, for "
", "
" but, in
fact for large values of "
", "
" is so smaller
than what seems from (13) inequality. But:
(14)
Proving (14) equality is possible with primary instruments.
8.1.10. Lemma
For every positive real number of "" and every natural
number of "k":
(15)
8.2. Prime numbers theorem
Research for measuring of "" is subject of a
lot of works and important resulted has been obtained in this field. Center of
researches was inquiry in prime numbers tables and comparison "" with
known functions. If you refer to little table:
|
x |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
10000 |
100000 |
1000000 |
10000000 |
100000000 |
|
|
25 |
46 |
62 |
78 |
95 |
109 |
125 |
139 |
154 |
168 |
1229 |
9592 |
78498 |
664579 |
5761455 |
And calculate "
", you can find that answer
is between "0.9" and "1.2" with this method. For first
time, relationship between "
" and "
" was
founded. First mathematicians who searched about "" were Legendre and
Gauss. Legendre (1798) said an assertion that for great value of "x":
(16)
Able described this assertion (a letter in 1832) as
"the most considerable theorem in all of mathematics". Gauss had
started his searches in this field apparently around the years 1792 and 1793,
and published firstly in 1863. Gauss as we saw in above little table, guessed
when "x" become great, the ratio of "" to "
",
approaches to "1" and in the other hand:
(17)
Also, he counted logarithmic integral of "x"
as better approximate value for "" from "".
But, none of two mentioned scientists could prove their tentative assertions.
The first mathematician who calculated a verified assertion
about behavior of "", was Chebyshev (1850). He
proved that "" is from order of "
". Exactly
he proved that If "x" be great sufficiently:
(18)
Also he proved that if mentioned limit exists in (17), it is equal to "1". But relation (17) remained as an enigma so that Riemann solved that problem in 1859. His demonstration to prove this relation isn’t perfect and enough. But it has necessary thought for a perfect demonstration. Finally, in (1896), "Hadamard and Poussin separately, proved relation (17) and this theorem which is famous as prime numbers theorem", is central core of prime numbers theorem. Hadamard and Poussin's demonstration is by means of complex function theorem and for many years, processes of this theorem is basic and inevitable to proving prime numbers theorem, so that in 1948, Selberg and Ardosh presented primary demonstration to this theorem and this had important effect between scientists of number theory. It is necessary to say that demonstrations are very complicated and detailed and primary description for them means its independence of complex functions theorem not in normal meaning.
What is said above was just for more information and will not be proved in this book. But we present Chebyshev’s theorem about natural numbers:
(19)
Its Proof is possible with primary instruments. Thinking
about below numbers is useful to comparison "
" function with below
functions:
.
8.3. The function"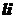
" or "the logarithmic
integral"
"li" function is defined by this equality:
(20)
That "c" is a constant number
. For abridge,
we write:
(21)
In below table, values 
and 
are written for some values of
"x".
Comparison table of "" and "
"
|
|
|
|
|
|
|
1000 |
168 |
178 |
0.94 |
1.159 |
|
10000 |
1229 |
1246 |
0.98 |
1.132 |
|
50000 |
5133 |
5167 |
0.993 |
1.111 |
|
100000 |
9592 |
9630 |
0.996 |
1.104 |
|
500000 |
41538 |
41606 |
0.9983 |
1.090 |
|
1000000 |
78498 |
78628 |
0.9983 |
1.084 |
|
2000000 |
148933 |
149055 |
0.9991 |
1.080 |
|
5000000 |
348513 |
348638 |
0.9996 |
1.075 |
|
10000000 |
664579 |
664918 |
0.9994 |
1.071 |
|
20000000 |
1270607 |
1270905 |
0.9997 |
1.068 |
|
90000000 |
5216954 |
5217810 |
0.99983 |
1.062 |
|
100000000 |
5761455 |
5762209 |
0.99986 |
1.061 |
|
1000000000 |
50847534 |
50849235 |
0.99996 |
1.053 |
It is proved:
(22)
It is wonderful that a simple function like "" shows
the irregular function "", so good (see 4th column).
In above table, always "
", but this assertion is not
general. In 1914, Littlewood proved that for
, "
" is infinitely
positive or negative. According to Skewes's researches (1933 and after that) a
number like "
" exists that is smaller than
and
.
8.3.1. Remark
Prime numbers theorem for arithmetical progression is that
If "a" and "m" be two considered coprime
natural numbers and be numbering of prime numbers in the form of "
" 
that aren’t
more than "x" then:
(23)
This theorem also, like prime numbers theorem is provable with primary way.
8.3.2. Remark
For every two real numbers "
" and "
" that
"
":
(24)
8.4. Meissel's formula for "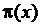
"
By presented formula Calculating "" is a tedious
work. In 1870, Meissel presented a formula for calculation of "" and
after long calculation, it resulted:
8.4.1. Example.
Calculating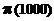
"
":
,
and 
…
From prime numbers table:
Therefore, according to Meissel's formula:
(25)
According to the prime numbers table:
,
So, according to (25):
(26)
To calculate 
we use from proved lemma:
According to other proved lemma:
Since 
and 
so according to before lemma:
So:
Then 
and therefore:
Subsequently:
168
8.4.2. Result
By now, we have remarked some of the most important results
about determining the number of prime numbers which are not more than a
supposed number "N", that most important one was
"Meissel’s formula" by which for determining the number of prime
numbers, "", all of prime numbers not
more than"
" and also the value of
"
"
for every "y" so that "
", should be determined
before.
Despite some modification in Meissel’s formula, done by
Lamer who prepared it to be calculated by electronic calculators, it is not
possible to apply it in scientific and practical manner and we have shown how
many acknowledged parameters should be used for calculation of
.
It is obvious that if "N"
is a great number, calculating the "" will be impossible. In
fact, we are seeking a simple relation that gives us the numbers of prime
numbers, not more than "N", with an acceptable estimation. It
is clear that because of the great gap between the prime numbers, it is
impossible to find a certain relation, by which the number of prime numbers can
be determined.