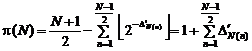CHAPTER 9

Decisive solution to the problem of determining of the precise number of "" primes by characteristic function""

 

 

9.1. Determining "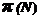" by ""

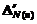We know that for determining the number of prime numbers,  not more than a arbitrary odd number "N", it is enough to  subtract a number equal to the sum of all odd composite numbers, not more than "N", from , because "1" is neither prime, nor composite, and in contrast "2" is only even prime number.

Function with formula  is defined as follow:

 

 

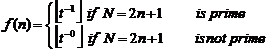
If "", the function will be defined as:

 

 

Therefore, function with the formula as below, gives the number of composite numbers not more than "N" and greater than "1":

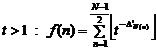
For simplification if suppose "", then the function "" can be defined as follow:

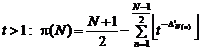        (1)

 

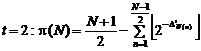        (2)

9.1.1. Example

We calculate the number of prime numbers not more than "17", using the formula:

                 

              

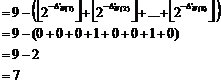
So:

9.1.2. Note

It is always possible to suppose that "N" is an odd number, because if "N" is even "".

Generally, for any arbitrary odd number, we can define a number like that is the representative of the number of prime numbers not more than "N", and it can be shown as the table follow:

 

N

3

5

7

9

11

13

15

17

19

…

2

3

4

4

5

6

6

7

8

…

 

Here, we will calculate and then we compare the resulted number with these limits as below and also with the number resulted by Meissel’s formula:

9.2. Comparing the precise formula for "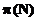"with
Meissel's formula

After a difficult and boring calculation with several parameters, we have gained the below number by the Meissel’s formula:

Because:

When applying Meissel’s formula, the parameter with a more difficulty to calculate than the others and specially for great values of "x", is impossible to be calculated, is "".

It is necessary to mention that Meissel’s formula can not be used after a great number like "N", because calculating the "" is as difficult as "".

Here, we calculate "" by "":

 

                     

                       

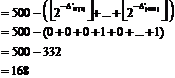
9.2.1. Note

For calculation a term containing "å", we simply write a software program so that it can result the calculation of very great number in a short time.

9.2.2. Remark

 If we show the number of odd composite numbers, not more than "N", by the symbol "", the relation (1) will be summarized as:

 

In fact, for calculating, it is necessary to write a program to calculate:

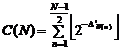
9.2.3. Remark

Function is defined in a more simplified form:

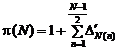       (3)

9.2.4. Note

The relations (2) and (3) are equal: