



 Table
of Contents :
Book of the discovery of prime numbers formula and its results
Table
of Contents :
Book of the discovery of prime numbers formula and its results



By


 Click
here to view the
chapter 1
of the book
Click
here to view the
chapter 1
of the book


 ----
Chapter 1
part A ----
Chapter 1 part B
----
Chapter 1
part A ----
Chapter 1 part B


 Click
here to view the
chapter 2
of the book
Click
here to view the
chapter 2
of the book





 Click
here to view the
chapter 3
of the book
Click
here to view the
chapter 3
of the book




San Carlos, 29 y 30 de julio de 2009
*Autodidacta en estudios matemáticos
En este trabajo se presenta una prueba de
primalidad basada en algunos
teoremas que permiten crear las bases para
su desarrollo y confiabilidad en
tiempo polinomial. En otras palabras
esta prueba de primalidad atiende el
problema sobre la determinación de si un
número (n) dado es primo o no, y de
igual forma se puede realizar un
algoritmo con el cual obtener un número primo
aleatorio dada una entrada.Cuestión que es
conocida como el problema de la
primalidad y todo esto nos conduce a
resolver de una manera sencilla este
roblema el cual es el objetivo de esta
investigación.
Palabras claves: prueba, algoritmo,
primo
Abstract
This paper presents a
primality test based on some theorems that allow to
create the
foundation for its development and reliability in polynomial
time. In
other words this
test of primality addresses the problem of determining if a
given number (n)
is prime or not, and like wise and algorithm can be designed
to
get a random
prime number, given an input. This fact is known as the
problem of
primality and all this
leads to simple way of solving this problem which is
the objective of
this research.
keywords: Test, Algorithm, Prime





Download The PDF File Of Primality
Test
https://studylib.es/doc/5773406/resumen-desarrollo-del-proceso-de-producción-de



 In order to
buy the PDF file
of The Discovery of
Prime Numbers Formula and Its Results book just send
ETH to amount of
0.066
to the Public Address of
0x62b59070BC3147f53a26AA935F6dB16B668ccd18
In order to
buy the PDF file
of The Discovery of
Prime Numbers Formula and Its Results book just send
ETH to amount of
0.066
to the Public Address of
0x62b59070BC3147f53a26AA935F6dB16B668ccd18


Public Address to Receive ETH
0x62b59070BC3147f53a26AA935F6dB16B668ccd18
Pay me via Trust Wallet:
https://link.trustwallet.com/send?coin=60&address=0x62b59070BC3147f53a26AA935F6dB16B668ccd18&amount=0.066
or any other wallet that you
trust.
 Notice:
Please send only Ethereum (ETH) to this address.
Notice:
Please send only Ethereum (ETH) to this address.
Sending any other coins may
result in permanent loss.


 Public Address of
0x62b59070BC3147f53a26AA935F6dB16B668ccd18
Public Address of
0x62b59070BC3147f53a26AA935F6dB16B668ccd18

 phone:
+995591041322
phone:
+995591041322
Weekdays 8:30am - 5:30pm GMT
through WhatsApp
vip.hashemi.moosavi@gmail.com
 Send your
Transaction Details
to Email
vip.hashemi.moosavi@gmail.com
or use
Send your
Transaction Details
to Email
vip.hashemi.moosavi@gmail.com
or use
the phone number through WhatsApp in order to
inform.

Book of the discovery of prime numbers formula and its results &
Other Top Researches
Price of the e-book is 121.00$
equals to 0.066 ETH that you should send it to the website
Wallet
with
Public Address of
 0x62b59070BC3147f53a26AA935F6dB16B668ccd18
0x62b59070BC3147f53a26AA935F6dB16B668ccd18
Product details
-
Publisher : Meraje Ghalam Publications (July 16,
2016)
-
Publication date : July 16, 2016
-
Language : English
- Print Length
: 344 pages
-
ISBN-10 : 6009446791
-
ISBN-13 : 9786009446797
- Item
Weight : 488 grams
- Best
Sellers Rank: #390631
www.primenumbersformula.com &
www.komhm.com
- Price: 121.00 $

last good news about
Alireza Magic Square

by Seyyed Alireza Hashemi Moosavi
Magic squares
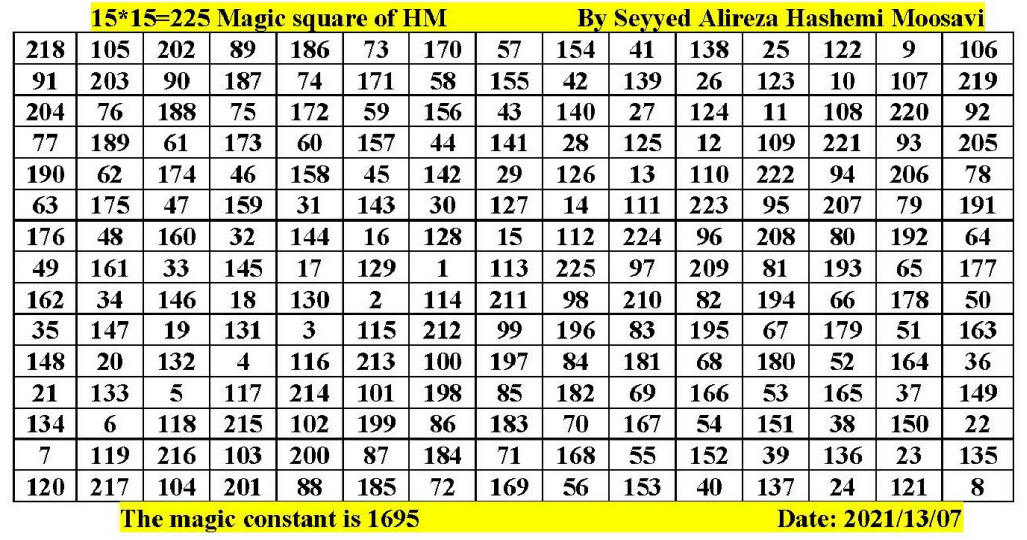
of Seyyed Alireza Hashemi Moosavi publish date: 2021/13/07
Magic square of 3 by 3 by Seyyed Alireza
Hashemi Moosavi

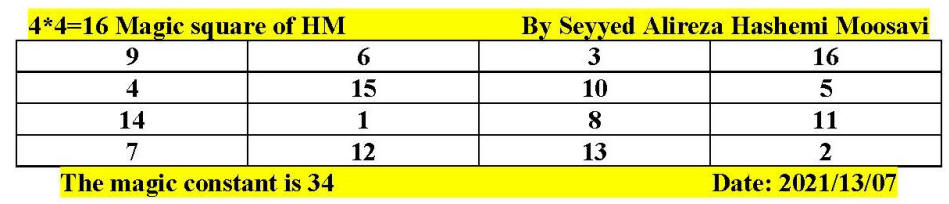
Magic square of 4 by 4 by Seyyed Alireza
Hashemi Moosavi
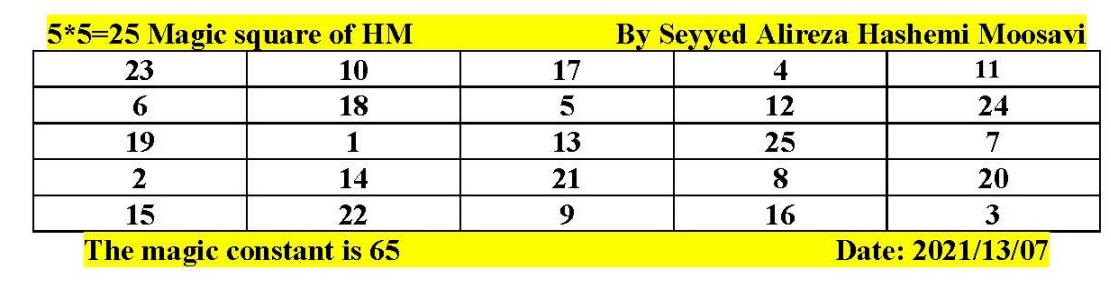
Magic square of 5 by 5 by Seyyed Alireza
Hashemi Moosavi
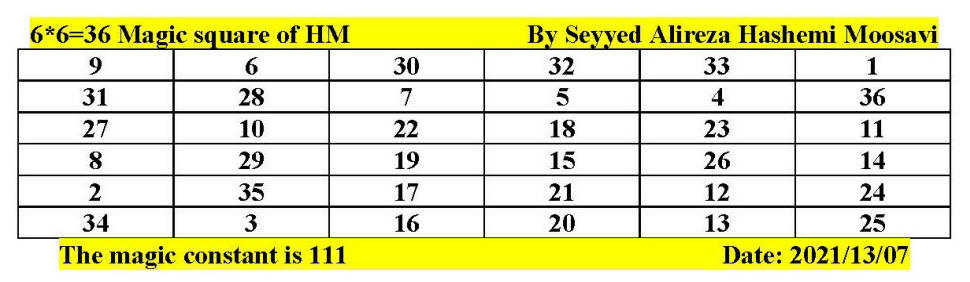
Magic square of 6 by 6 by Seyyed Alireza
Hashemi Moosavi
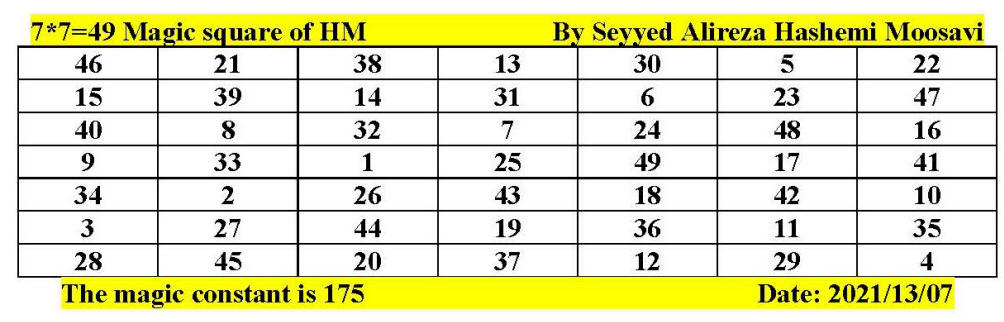
Magic square of 7 by 7 by Seyyed Alireza
Hashemi Moosavi
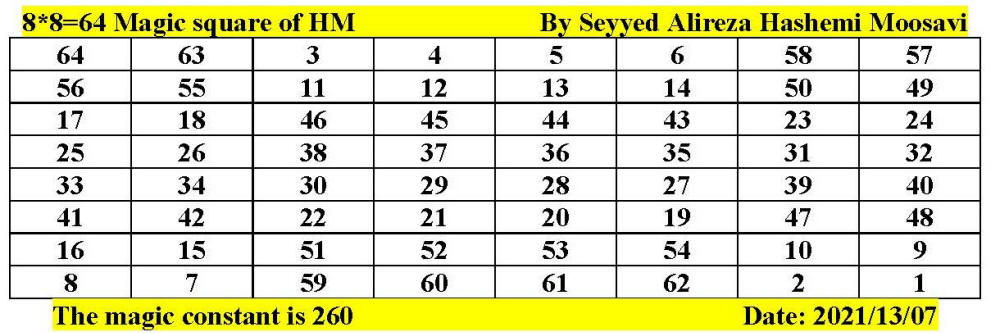
Magic square of 8 by 8 by Seyyed Alireza
Hashemi Moosavi
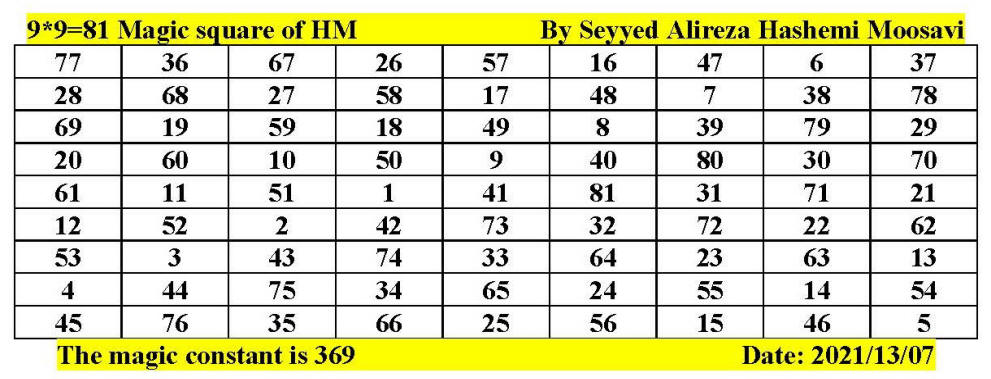
Magic square of 9 by 9 by Seyyed Alireza
Hashemi Moosavi
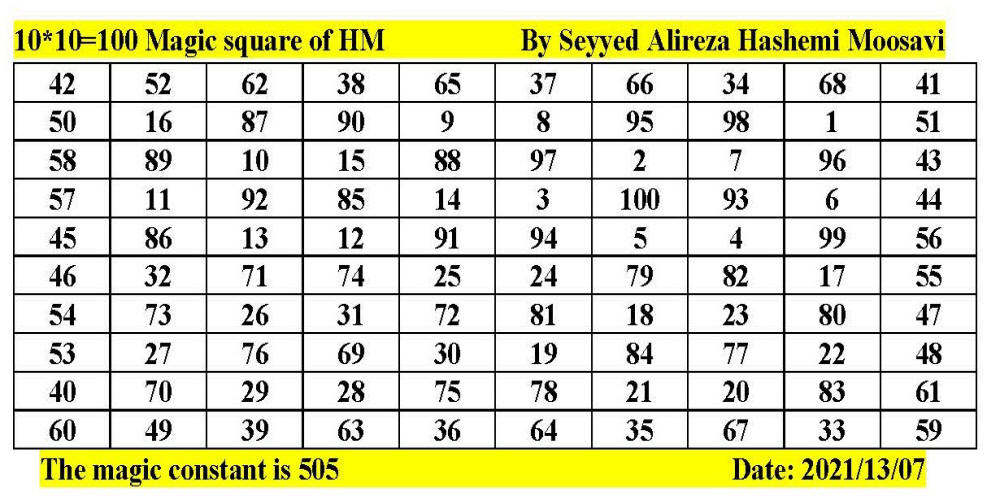
Magic square of 10 by 10 by Seyyed Alireza
Hashemi Moosavi
Magic square of 11 by 11 by Seyyed Alireza
Hashemi Moosavi
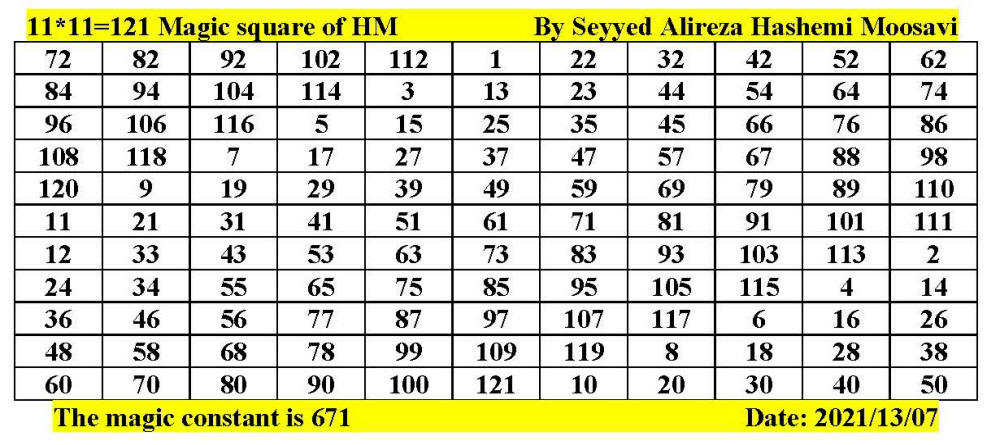
Magic square of 12 by 12 by Seyyed Alireza
Hashemi Moosavi
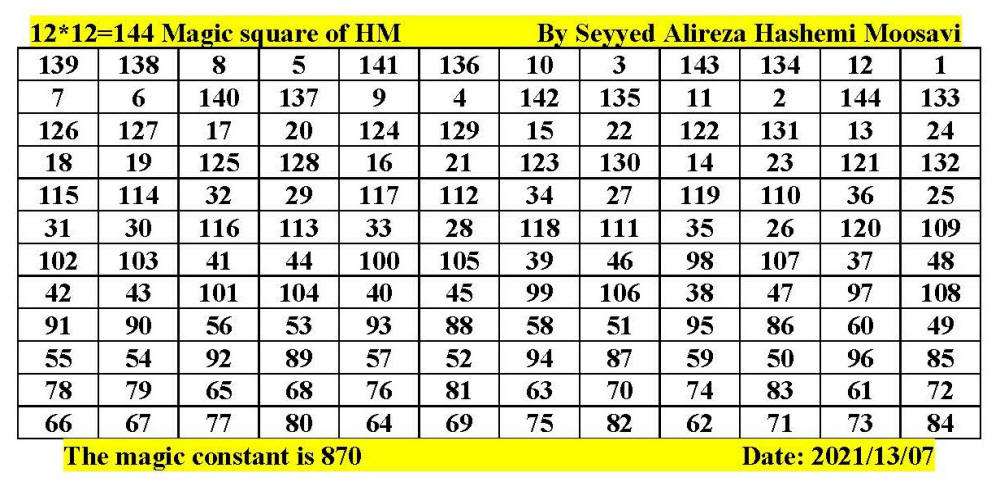
Magic square of 13 by 13 by Seyyed Alireza
Hashemi Moosavi
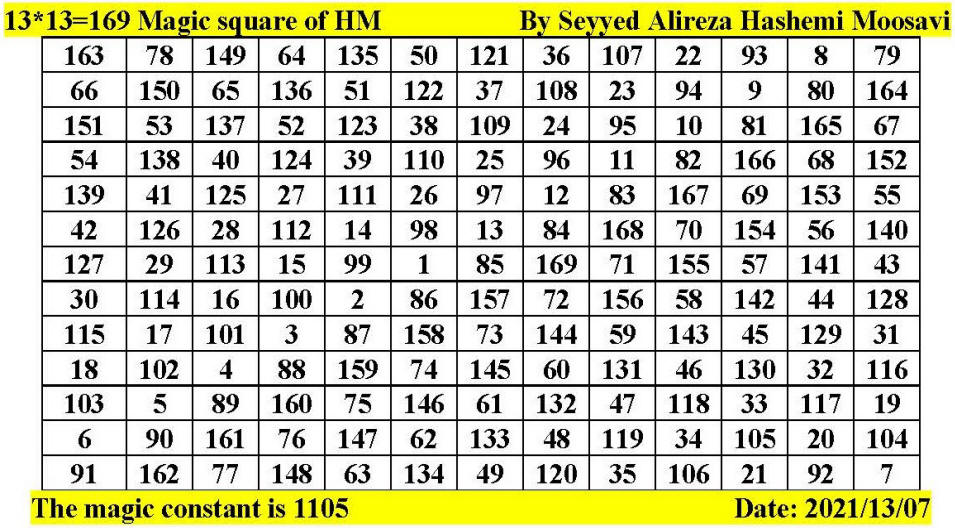
Magic square of 14 by 14 by Seyyed Alireza
Hashemi Moosavi
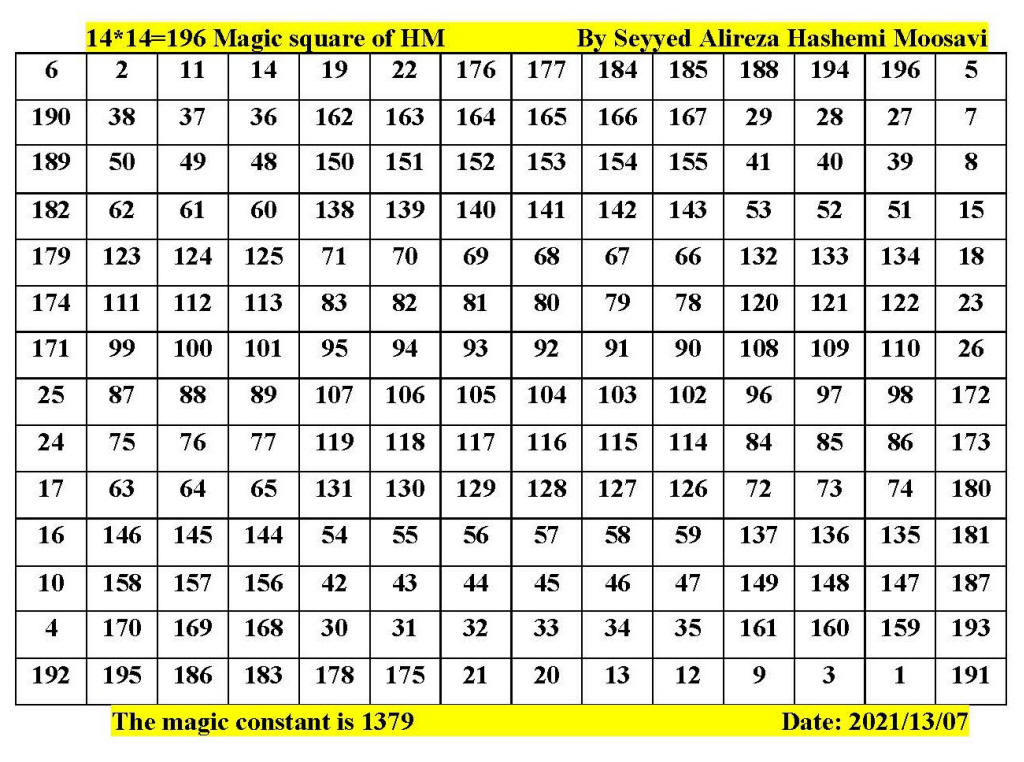
Magic square of 15 by 15 by Seyyed Alireza
Hashemi Moosavi





 You
can check the address to find the list below
You
can check the address to find the list below




http://www.topmillion.net/domain-list-333
\

Notice:
Unfortunately there is something
that you can understand but I don't
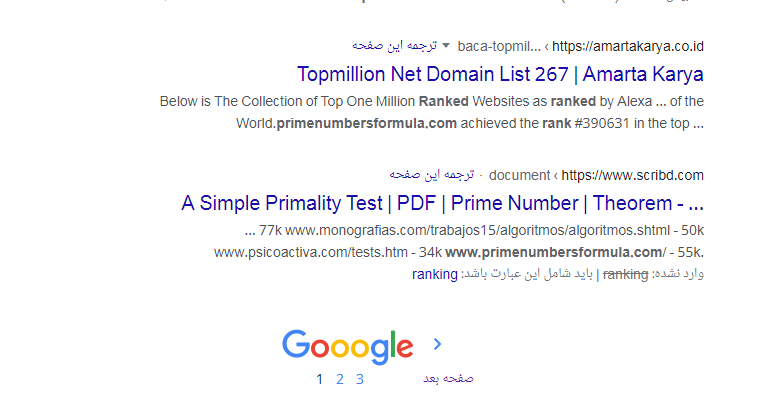
Alexa ranking of top million list of 1,000,000 Websites of the World
that
www.primenumbersformula.com in
the year of 2022 could
achieve the rank
of
#390631 in the top one
million websites of the world.

 You can freely download
PDF file of chapter 1 .
You can freely download
PDF file of chapter 1 . Book of the discovery of prime numbers formula and its results
Book of the discovery of prime numbers formula and its results
 You can freely download
PDF
file of chapter 2
.
You can freely download
PDF
file of chapter 2
.
 Book of the discovery of prime numbers formula and its results
Book of the discovery of prime numbers formula and its results
 You can freely download
PDF
file of chapter 3
.
You can freely download
PDF
file of chapter 3
.
 Book of the discovery of prime numbers
formula and its results
Book of the discovery of prime numbers
formula and its results


